Материал из Linuxformat.

R Свободный инструментарий для статистического анализа на реальных примерах

Содержание 1 R: Размножаем реальность 1.1 Задача 1.2 Реальные условия 1.3 Решение 1.4 Техническое исполнение 1.5 Уточнение задачи 1.6 Результат

R: Размножаем реальность

R
Часть 1: Введение в R Часть 2: Данные и графики Часть 3: Мир с точки зрения R Часть 4: Анализ данных с R Часть 5: Работа с двумя переменными Часть 6: Взаимосвязь случайных величин Часть 7: Графические интерфейсы Часть 8: Интеллектуальный анализ, или Data Mining

R на примере
R: Размножаем реальность R: GUI на примере R: Ускоряем на примере R: Поиск закономерностей

Довольно легко оценить эффективность хоккеиста по числу забитых голов и голевых передач, но что делать в более сложных случаях? Евгений Балдин и Сергей Петров оценивают эффективность рассылки спама…

Ну, не совсем того спама, о котором вы, вероятно, подумали. Рассылка осуществлялась университетом с целью проинформировать абитуриентов о своём существовании. Общаясь с будущими студентами, можно заметить одну очень любопытную особенность: выбор высшего учебного заведения и уж тем более факультета зачастую делается достаточно случайным образом. Безусловно, есть группа молодых людей, которые почти с раннего детства знают, куда поступать, но большинство об этом моменте почему-то серьёзно особо не задумываются. Очевидно, что абсолютно всех абитуриентов конкретного высшего учебного заведения объединяет одно: они все об этом вузе знают.

Задача

Факультет математики и информатики Гродненского государственного университета имени Янки Купалы (ГрГУ им. Я. Купалы) рассылал потенциальным абитуриентам (не кому попало, а именно подходящим для обучения на данном факультете молодым людям) письма-приглашения к поступлению. Необходимо было количественно оценить экономическую эффективность такой деятельности.

Эта проблема не нова, так как реклама является необходимым инструментом стимулирования продаж. С течением времени на получение одинакового покупательского отклика необходимо тратить на рекламу всё больше средств и при этом диверсифицировать каналы её распространения. Отсюда естественно желание, в нашем случае, руководства вуза оптимизировать затраты на рекламу на базе разумных расчётов, учитывающих реальность конкретной ситуации, а не идеальную модель из учебника. За эту задачу взялись сотрудники университета Ю.А. Войтукевич, В.Е. Лявшук и С.В. Петров.

Реальные условия

В 2009 г. в эксперимент по повышению качества абитуриентов «на входе» в образовательный процесс в ГрГУ им. Я. Купалы включился физико-технический факультет. Для определения целевой аудитории рекламной рассылки при помощи методов многомерной статистики были одновременно проанализированы результаты тестов по физике и математике 4116 абитуриентов. Из них для списка рассылки по указанной выше методике было отобрано 598 потенциальных кандидатов к поступлению на факультет, которым были высланы персональные (то есть с указанием фамилии, имени, отчества) приглашения к поступлению на физтех ГрГУ. Число 598 определялось ограничениями бюджета на рекламную кампанию. По итогам приемной кампании 2009 г. на физико-технический факультет было принято 146 абитуриентов, 61 из них в свое время получил персональное письмо-приглашение. Теперь хочется оценить количественный эффект от персонифицированной рассылки, если, естественно, он есть.

Оценка эффективности рекламы является весьма нетривиальной задачей. Рекламодатель всегда может точно указать величину запланированных или уже сделанных расходов на рекламу. А вот с оценкой величины не только будущего, но даже уже имеющегося эффекта от кампании у него обычно возникают трудности. Более-менее ясную картину можно получить в ситуации вывода на рынок абсолютно нового товара/услуги («истинной новинки»), когда информирование покупателей начинается «с нуля». В остальных же случаях сложно определить, сколько покупателей пришло за покупкой под влиянием конкретной рекламы по конкретному каналу распространения информации, а сколько – под действием иных факторов. В то же время, только точное определение величины эффекта от воздействия конкретного канала распространения рекламы позволяет адекватно планировать, контролировать и вовремя корректировать рекламную кампанию.

Решение

Если мы знаем количество откликов в результате проведенной кампании и количество контактов потенциальных покупателей с определенным каналом распространения рекламы, то можем, построив статистическую модель случайного поведения покупателей, многократно (пусть «многократно» – это 10 тысяч и более раз) сравнить реальную картину поведения покупателей с моделью. Тогда удастся с какой-то точностью оценить, сколько покупателей приняло решение о покупке под влиянием рекламы по конкретному каналу.

Фактически, выше сформулирована задача для метода размножения выборок или бутстреп-анализа (bootstrap resampling technique, или bootsrapping). Этот метод был предложен американским статистиком Брэдли Эфроном [Bradley Efron] в 1977 году. Он отличается от традиционных методов статистического анализа тем, что предполагает многократную обработку различных частей одних и тех же данных, как бы поворот их «разными гранями», и сопоставление полученных таким образом результатов. Бутстреп-процедура не требует информации о виде закона распределения изучаемой случайной величины, и в этом смысле может рассматриваться как метод непараметрической статистики.

При некоторой фантазии, вспомнив о подвигах барона Мюнхгаузена, «bootstrap» можно перевести как «вытягивание себя из болота за шнурки от ботинок». Что, собственно говоря, мы и делаем. Число 10 000 взято неспроста: бутстреп-процедура позволяет лишь асимптотически приблизиться к верному ответу, поэтому число тестов должно быть очень большим.

Есть мнение, что использовать бутстреппинг истинный исследователь будет только от полной безнадёжности, и если имеются хоть какие-нибудь рабочие гипотезы, позволяющие предсказать по ведение модели, то лучше заняться их развитием. Предположим, что таковые гипотезы у нас отсутствуют или нам просто лень их развивать.

Рассчитаем, насколько полученный результат приёмной кампании близок к случайному. Очевидно, что для этого достаточно рассчитать распределение вероятности количества принятых абитуриентов, получивших письмо-приглашение в численном эксперименте, по случайной рассылке 598 писем.

Для этого случайным образом выбираем 598 человек из 4165 возможных кандидатов и проверяем, сколько среди них находится тех, кто действительно поступил на физический факультет. Данный эксперимент повторяем 10 тысяч раз и строим распределение числа выбранных таким образом людей, поступивших на факультет. Данные 10 тысяч попыток позволяют построить распределение числа поступивших абитуриентов, получивших письмо-приглашение случайным образом.

Техническое исполнение

На языке среды статистических расчетов R данная задача выглядит примерно следующим образом:

# Обнуляем вектор результатов
> bstr <- 1
# Записываем в вектор результатов 10000 вариантов
# попадания писем абитуриентам (крутим цикл)
> for (n in 1:10000) {
# На каждом шаге выбираем 598 случайных абитуриентов из 4116
# и подсчитываем, сколько из них оказались в числе принятых
+ bstr[n] <- nrow(merge(
+ abitura[sample(1:4116, 598, replace= FALSE),], priem,
+ by.x=c(“Фамилия”,”Имя”,”Отчество”),
+ by.y=c(“Фамилия”,”Имя”,”Отчество”)))
+ }
# Строим гистограмму распределения числа поступивших
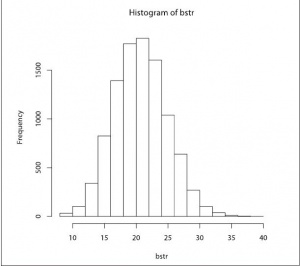
> hist(bstr)

Разберём, что было сделано, чуть-чуть поподробнее. Команда sample отбирает случайным образом из таблицы данных abitura 598 случайных абитуриентов. Команда merge сливает полученную выборку и таблицу данных priem по уникальному ключу, составленному из Фамилии, Имени и Отчества. При этом требуется наличие уникального ключа в обоих выборках. Команда nrow просто подсчитывает число совпавших в обоих списках (случайная выборка из всех потенциальных абитуриентов, сдававших тест, и список поступивших) абитуриентов.

На рис. 1 представлена гистограмма, составленная по результатам 10 000 попыток в ходе бутстрепа, в случае случайной рассылки 598 писем среди 4165 человек. Из рисунка очевидно, что вероятность получить среди зачисленных абитуриентов более 37 человек с таким письмом-приглашением составляет менее 0,1 %. Напоминаем, что таких на самом деле было 61 человек. На этом простом модельном эксперименте мы показали, что рассылка работает. При выполнении вышеописанной операции делается масса допущений, которые наверняка искажают результаты анализа, но мы договорилось, что это делается «от полной безнадёжности».

Уточнение задачи

Однако рассылать письма-приглашения всем без исключения абитуриентам, которые сдавали тест, не очень осмысленно. Поэтому в качестве следующего шага изучим распределения плотности вероятности количества поступивших абитуриентов в случае рассылки приглашений с отбрасыванием всех абитуриентов, имеющих оценки ниже установленного минимума.

Каждый из потенциальных абитуриентов сдавал тесты по физике и математике. В таблице данных abitura эти баллы нормируются к максимальному таким образом, что «волшебное число» абитуриентов 598 имеет балл больше 1 и по физике, и по математике, а минимальная оптимальная граница требований лежит в районе 0 (таких примерно четверть, а остальные три четверти проходивших тестирование имеют отрицательные результаты). То, как это было сделано, выходит за рамки данной статьи.

Оформим функцию бутстреп-эксперимента с двумя параметрами, характеризующими минимальные границы по физике и математике.

# Определяем функцию boot.fiz.mat.
# fiz.min – граница отсева по физике,
# mat.min – граница отсева по математике.
> boot.fiz.mat <- function (fiz.min, mat.min) {
# Обнуляем вектор
+ bstr <- 1
# Подсчитываем число потенциальных абитуриентов,
# удовлетворяющих условиям отбора
+ nn <- nrow(abitura[abitura[,”физика”]> fiz.min &
+ abitura[,”математика”]> mat.min,])
# Крутим цикл
+ for (n in 1:10000) {
# На каждом шаге выбираем 598 случайных абитуриентов
# из числа прошедших отбор и подсчитываем,
# сколько из них оказались в числе принятых
+ bstr[n] <- nrow(merge(
+ abitura[abitura[,”физика”]> fiz.min &
+ abitura[,”математика”]> mat.min,]
+ [sample(1:nn, 598, replace= FALSE),], priem,
+ by.x=c(“Фамилия”,”Имя”,”Отчество”),
+ by.y=c(“Фамилия”,”Имя”,”Отчество”)))
+ }
# Возвращаем результат
+ bstr}

Теперь проводим пять бутстреп-экспериментов, последовательно повышая границу отсева абитуриентов:

> bstr0 <- boot.fiz.mat(0, 0.)
> bstr02 <- boot.fiz.mat(0.2, 0.2)
> bstr04 <- boot.fiz.mat(0.4, 0.4)
> bstr06 <- boot.fiz.mat(0.6, 0.6)
> bstr08 <- boot.fiz.mat(0.8, 0.8)

и отображаем полученные результаты:

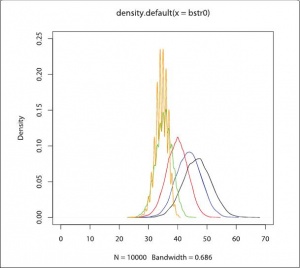
plot(density(bstr0),xlim=c(0,70),ylim=c(0,0.25),col=”black”)
lines(density(bstr02),col=”blue”)
lines(density(bstr04),col=”red”)
lines(density(bstr06),col=”green”)
lines(density(bstr08),col=”orange”)

Следует отметить, что процедура эта не из быстрых. Даже на такой не слишком большой выборке на более-менее современном персональном компьютере счёт идёт на десятки минут.

Из рис. 2 видно, что при повышении уровня требований от оптимальной границы среднее смещается влево. Это показывает, что процедура отсечения только по баллам является недостаточно эффективной по сравнению с используемой при рассылке. Даже в самом удачном случае (чёрный график) вероятность получить в числе зачисленных 61 и более абитуриентов с письмом-приглашением составляет менее 0,0022 (22 случая на 10 000 попыток). Этот практически крайний случай задан оптимальной нижней границей требований. Все другие случаи отсечения абитуриентов по нижней границе результатов тестирования дают ещё меньшую вероятность получить на выходе 61 отклик. Но даже распределение с оптимальной нижней границей демонстрирует максимальную плотность вероятности в районе 46 человек. Это говорит о крайне высокой достоверности наличия эффекта рассылаемых писем-приглашений.

Попробуем теперь оценить эффект от рассылки количественно. Для этого немного изменим график, построив распределение разницы между числом фактически принятых во время вступительной кампании 2009 г. абитуриентов, получивших приглашение, и эффектом от случайной рассылки:

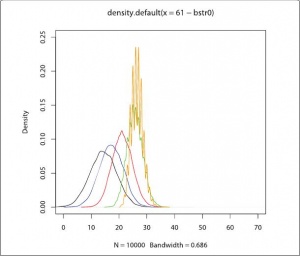
plot(density(61-bstr0),xlim=c(0,70),ylim=c(0,0.25),col=”black”)
lines(density(61-bstr02),col=”blue”)
lines(density(61-bstr04),col=”red”)
lines(density(61-bstr06),col=”green”)
lines(density(61-bstr08),col=”orange”)

Результат

На рис. 3 отражена картина, когда от реального результата приемной кампании (61 абитуриент с письмом-приглашением в числе 146 зачисленных) отнимаются гипотетические результаты, которые можно получить в результате случайной рассылки 598 приглашений всем, чьи результаты выше оптимальной границы требований. Видно, что разница между реальным и гипотетически наиболее вероятным результатом равна примерно 15. Это именно те пятнадцать человек, о которых можно сказать, что они пришли на факультет исключительно благодаря целенаправленной рассылке писем-приглашений.

Для пятнадцати человек письмо-приглашение сыграло роль последнего импульса к принятию решения. Естественно, мы не имеем возможности определить эти пятнадцать по фамилиям, но в эффекте целенаправленной рассылки мы в какой-то степени уверены. Зная, сколько денег пошло на мероприятие, теперь легко оценить, сколько ресурсов было потрачено на одного качественного дополнительного абитуриента. В пересчёте с белорусских рублей на российские, затраты в данном случае составляли около 250 рублей на одного хорошего человека. Много это или мало – решать заказчику.

Да, то, что рассылка эффективна, на самом деле было установлено опытным путём. В 2009 году факультет математики и информатики отказался от практики рассылки, а физико-технический факультет воспользовался этими наработками и впервые за многие годы получил достоверно более качественный набор, чем слишком поздно пожалевшие о своём неправильном шаге математики. Обычно на физику идут не так активно, как на математику, по причине того, что физики в школе гораздо меньше, чем математики, не говоря уж об информатике. Так что множество наукообразных слов, составляющих эту статью, на самом деле в какой-то степени верны. Экспериментальный факт.