- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF109:R
Материал из Linuxformat.
- R Свободный инструментарий для статистической обработки данных
Содержание |
Работа с двумя переменными
| R |
|---|
| R на примере |
|---|
- Повествование об R возобновляется на новом уровне. С января по апрель этого года мы провели предварительный обзор возможностей, а теперь Антону Коробейникову и Евгению Балдину предстоит настоящая работа.
ЧАСТЬ 1 Проверка гипотез однородности
Две разные выборки называются однородными, если они одинаково распределены. Проверка «гипотез однородности» в математической статистике занимает особое место. Этот факт связан с тем, что для практических приложений, как правило, характерны задачи сравнения двух и более групп наблюдений. Сравнивать выборки можно совершенно разными способами: исследователя может интересовать различие в средних, медианах, дисперсиях при разнообразных предположениях относительно самих наблюдений.
Параметрические критерии проверки однородности выборок
Величины, имеющие нормальное распределение, возникают в реальных экспериментах совершенно естественным образом. При измерении любой характеристики всегда имеется ошибка измерения. Если предположить, что погрешность прибора имеет нормальное распределение, то среднее отвечает за систематическую ошибку, а дисперсия – за величину случайной ошибки. Поэтому критерии, представленные в данном разделе учебника, предполагают, что выборка имеет нормальное распределение. Если это заранее не известно, то данный факт нужно проверять отдельно (см. Проверка гипотез нормальности распределения ниже). В противном случае все выводы, полученные на основе этих критериев, будут ошибочными.
- Двухвыборочный критерий Стьюдента равенства средних
Двухвыборочный t-критерий используется для проверки гипотезы о равенстве средних в двух независимых выборках, имеющих нормальное распределение. В своей классической постановке критерий приводится в предположении равенства дисперсий. Однако в R реализована его модификация, позволяющая избавиться от данногопредположения.
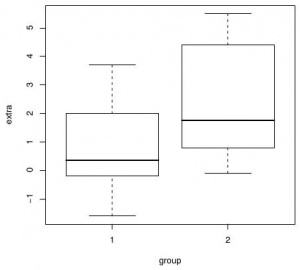
Воспользуемся классическим набором данных, который фигурировал ещё в оригинальной статье Стьюдента (псевдоним Вильяма Сили Госсета [William Sealy Gosset]). В упомянутой работе производилось сравнение влияния двух различных снотворных на увеличение продолжительности сна (см. рис. 1). В R этот массив данных доступен под названием sleep в пакете stats. В столбце extra содержится среднее приращение продолжительности сна после начала приёма лекарства (по отношению к контрольной группе), а в столбце group – код лекарства (первое или второе).
> plot(extra ~ group, data = sleep)
Влияние лекарства на каждого человека индивидуально, но среднее увеличение продолжительности сна можно считать вполне логичным показателем «силы» препарата. Основываясь на этом предположении, попробуем проверить при помощи t-критерия, значимо ли различие в средних для двух этих выборок (соответствующих двум разным лекарствам):
> with(sleep, t.test(extra[group == 1],
+ extra[group == 2], var.equal = FALSE))
Welch Two Sample t-test
data: extra[group == 1] and extra[group == 2]
t = -1.8608, df = 17.776, p-value = 0.0794
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.3654832 0.2054832
sample estimates:
mean of x mean of y
0.75 2.33
Параметр var.equal позволяет выбрать желаемый вариант критерия: оригинальный t-критерий Стьюдента в предположении одинаковых дисперсий (TRUE) или же t-критерий в модификации Уэлча [Welch], свободный от данного предположения (FALSE).
Хотя формально гипотеза о равенстве средних не отвергается на стандартных уровнях значимости, мы видим, что возвращаемое p-значение (0.0794) достаточно маленькое, поэтому к данном результату следует отнестись критически. Это означает, что, возможно, стоит попробовать другие методы для проверки гипотезы, увеличить количество наблюдений, ещё раз убедиться в нормальности распределений, и т.д.
Можно ли использовать t-критерий, если необходимо сравнить среднее в зависимых выборках (например, при сравнении какого-либо жизненного показателя у пациента до и после лечения)? Ответ на этот вопрос: «Да, можно, но не обычный, а модифицированный специальным образом под такую процедуру». В литературе это известно как парный t-критерий. Для использования парного t-критерия в R достаточно выставить опцию paired в TRUE:
> with(sleep, t.test(extra[group == 1],
+ extra[group == 2], paired = TRUE))
Paired t-test
data: extra[group == 1] and extra[group == 2]
t = -4.0621, df = 9, p-value = 0.002833
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.4598858 -0.7001142
sample estimates:
mean of the differences
-1.58
Здесь видно, что парный t-критерий отвергает гипотезу о равенстве средних с достаточно большой надёжностью. Следует отметить, что использованные в этом примере выборки не были «парными», поэтому, строго говоря, применять парный t-критерий нельзя, так что все выводы носят сугубо иллюстративный характер.
- Двухвыборочный критерий Фишера равенства дисперсий
Естественной характеристикой «размаха» распределения при нормальной модели является дисперсия. Предположим, что нам потребовалось проверить гипотезу об отсутствии различий в дисперсиях двух выборок, и при этом не хочется делать абсолютно никаких допущений относительно значений средних. Такая задача может возникнуть, например, при сравнении точности двух приборов. Систематическую ошибку иногда можно уменьшить за счёт лучшей калибровки, случайную же погрешность убрать почти никогда нельзя. В связи с этим задача проверки равенства дисперсий (например, при сравнении эталонного и поверяемого приборов) становится достаточно актуальной.
Решением такой задачи служит F-критерий Фишера [Fisher]. В R он реализован в функции var.test():
> x <- rnorm(50, mean = 0, sd = 2);
> y <- rnorm(30, mean = 1, sd = 1);
> var.test(x, y)
F test to compare two variances
data: x and y
F = 3.8414, num df = 49, denom df = 29, p-value = 0.0002308
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
1.930003 7.227256
sample estimates:
ratio of variances
3.841391
В данном примере участвуют две выборки с разным количеством наблюдений (50 и 30 для x и y, соответственно), разными средними (0 и 1) и дисперсиями (22=4 и 12=1). Гипотеза о равенстве дисперсий безусловно отвергается (p-значение мало). Кроме самого значения тестовой статистики, p-значения и величин степеней свободы, функция выводит оценку отношения дисперсий и доверительный интервал от него. Значение оценки 3.55 не очень сильно отличается от истинного значения отношения дисперсий 4.
На самом деле, критерий проверяет несколько более общую гипотезу, а именно, что отношение дисперсий двух выборок имеет какое-то наперёд заданное значение. Очевидно, равенство дисперсий является её частным случаем.
Предполагаемое значение отношения дисперсий можно задать с помощью опции ratio:
> x <- rnorm(50, mean = 0, sd = 2);
> y <- rnorm(30, mean = 1, sd = 1);
> var.test(x, y, ratio = 4)
F test to compare two variances
data: x and y
F = 1.1097, num df = 49, denom df = 29, p-value = 0.7778
alternative hypothesis: true ratio of variances is not equal to 4
95 percent confidence interval:
2.230136 8.351157
sample estimates:
ratio of variances
4.43876
Здесь видно, что при задании истинного значения отношения дисперсий гипотеза не отвергается.
Непараметрические критерии проверки однородности выборок
Критерии, приведённые в предыдущем разделе, работают только в предположении нормальности распределения данных. А что делать, если заранее известно, что выборки имеют другое распределение, или по каким-либо причинам проверить нормальность не получается? В таких случаях используются так называемые непараметрические критерии, т.е. критерии, свободные от предположения какой-либо параметрической модели данных. Естественно, ввиду того, что они оперируют гораздо меньшим «объёмом информации», эти критерии не смогут заметить те тонкие различия, которые были бы обнаружены при использовании их параметрических аналогов.
- Критерий Вилкоксона
Критерий Вилкоксона [Wilcoxon], двухвыборочный вариант которого ещё известен под именем критерия Манна–Уитни, является непараметрическим аналогом t-критерия.
Стандартный набор данных airquality содержит информацию о количестве озона в воздухе города Нью-Йорка с мая по сентябрь 1973 года. Проверим, например, гипотезу о том, что распределения уровня озона в мае и в августе было одинаковым:
> wilcox.test(Ozone ~ Month, data = airquality,
+ subset = Month %in% c(5, 8))
Wilcoxon rank sum test with continuity correction
data: Ozone by Month
W = 127.5, p-value = 0.0001208
alternative hypothesis: true location shift is not equal to 0
Критерий отвергает гипотезу о согласии распределений уровня озона в мае и в августе с достаточно большой надёжностью. В принципе, это достаточно легко вытекает из «общих соображений», т.к. как уровень озона в воздухе сильно зависит от солнечной активности, температуры и ветра. И если с солнечной активностью всё в порядке:
> wilcox.test(Solar.R ~ Month, data = airquality,
+ subset = Month %in% c(5, 8))
Wilcoxon rank sum test with continuity correction
data: Solar.R by Month
W = 422.5, p-value = 0.4588
alternative hypothesis: true location shift is not equal to 0
то распределения ветра и температуры, напротив, сильно различаются:
> wilcox.test(Temp ~ Month, data = airquality,
+ subset = Month %in% c(5, 8))
Wilcoxon rank sum test with continuity correction
data: Temp by Month
W = 27, p-value = 1.747e-10
alternative hypothesis: true location shift is not equal to 0
> wilcox.test(Wind ~ Month, data = airquality,
+ subset = Month %in% c(5, 8))
Wilcoxon rank sum test with continuity correction
data: Wind by Month
W = 687.5, p-value = 0.003574
alternative hypothesis: true location shift is not equal to 0
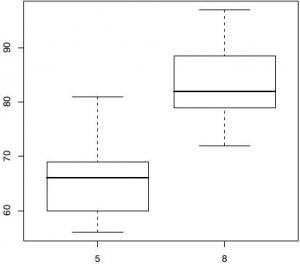
Эти различия хорошо видны, скажем, на изображении «ящиков с усами» (рис.2):
> boxplot(Temp ~ Month, data = airquality, + subset = Month %in% c(5, 8))
но в более сложных случаях объективные результаты можно получить только с использованием критериев.
По умолчанию, критерий проверяет гипотезу о том, что распределения двух выборок отличаются лишь постоянным и известным сдвигом (который, в свою очередь, по умолчанию равен нулю). Задать его можно при помощи параметра mu. Например:
> x <- rnorm(50, mean = 0);
> y <- rnorm(50, mean = 2);
> wilcox.test(x, y);
Wilcoxon rank sum test with continuity correction
data: x and y
W = 230, p-value = 2.091e-12
alternative hypothesis: true location shift is not equal to 0
> wilcox.test(x, y, mu = -2);
Wilcoxon rank sum test with continuity correction
data: x and y
W = 1335, p-value = 0.5602
alternative hypothesis: true location shift is not equal to -2
Критерий Манна–Уитни, как и t-критерий, бывает парным. Для использования парной модификации необходимо выставить опцию paired в значение TRUE. Задание опции conf.int позволяет получить оценку различия в сдвиге между двумя выборками (естественно, при условии, что кроме сдвига, распределения двух выборок ничем не отличаются) и доверительный интервал для него:
> x <- rnorm(50, mean = 0);
> y <- rnorm(50, mean = 2);
> wilcox.test(x, y, conf.int = TRUE);
Wilcoxon rank sum test with continuity correction
data: x and y
W = 227, p-value = 1.803e-12
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
-2.418617 -1.500210
sample estimates:
difference in location
-1.941988
> wilcox.test(x, y, mu = -2);
Wilcoxon rank sum test with continuity correction
data: x and y
W = 1292, p-value = 0.7748
alternative hypothesis: true location shift is not equal to -2
Гипотеза о полном равенстве распределений была отвергнута, а гипотеза о том, что одно распределение отличает от другого просто сдвигом – принята, что и требовалось доказать.
- Непараметрические критерии сравнения масштаба
Дисперсия является естественным параметром масштаба для выборки из нормальной совокупности. Этот факт в случае нормального распределения и позволяет заменить гипотезу о совпадении масштабов на гипотезу о совпадении дисперсий. При отказе от нормальной модели дисперсия уже не является характеристикой масштаба, и поэтому надо честно проверять гипотезу именно о совпадении масштабов распределений двух выборок.
Формально предполагается, что одна из выборок имеет распределение с плотностью f(x-a), другая – s*f(s*(x-a)). Здесь функция плотности f и параметр сдвига a считаются неизвестными. Мы заинтересованы в проверке совпадения масштабов у двух выборок, т.е. того, что s=1.
В стандартном пакете stats реализованы два классических непараметрических критерия, позволяющих проверить равенство масштабов: критерий Ансари–Брэдли [Ansari–Bradley] и критерий Муда [Mood]. Начнём с первого.
> ansari.test(runif(50), rucunif(50, max = 2))
Ansari-Bradley test
data: runif(50) and runif(50, max = 2)
AB = 1404, p-value = 0.07526
alternative hypothesis: true ratio of scales is not equal to 1
Распределение выборок в данном случае отличается только масштабом. Критерий отвергает гипотезу о совпадении дисперсий на стандартных уровнях значимости, как это и должно быть. Для критерия Муда всё аналогично:
> mood.test(runif(50), runif(50, max = 2))
Mood two-sample test of scale
data: runif(50) and runif(50, max = 2)
Z = -2.5685, p-value = 0.01021
alternative hypothesis: two.sided
ЧАСТЬ 2 Проверка гипотез нормальности распределения
Большая часть инструментов статистического вывода работает в предположении о том, что выборка получена из нормальной совокупности. За примерами далеко ходить не надо: t-критерий, критерий Фишера, построение доверительных интервалов для линейной регрессии и проверка гипотезы о линейной независимости двух выборок.
Как уже отмечалось ранее, нормальное распределение естественным образом возникает практически везде, где речь идёт об измерении с ошибками. Более того, в силу центральной предельной теоремы, распределение многих выборочных величин (например, выборочного среднего) при достаточно больших объёмах выборки хорошо аппроксимируется нормальным распределением, вне зависимости от исходного распределения.
В связи с этим становится понятным, почему проверке распределения на нормальность стоит уделить особое внимание. В дальнейшем речь пойдёт о так называемых критериях согласия (goodness-of-fit tests). Проверяться будет не просто факт согласия с нормальным распределением с определёнными фиксированными значениями параметров, а несколько более общий факт принадлежности распределения к семейству нормальных со всевозможными значениями параметров.
Основные классические критерии проверки на нормальность собраны в пакете nortest. Его можно установить со CRAN при помощи вызова функции install.packages():
> install.packages(pkgs=c(«nortest»))
При этом будет предложено выбрать зеркало для загрузки файла Подключить установленный пакет можно при помощи функции library():
> library(nortest)
Может возникнуть вопрос: «А зачем так много разных критериев для проверки одного факта? Нельзя ли выбрать наилучший и всегда его использовать?». Ответ неутешителен: «В общем случае, к сожалению, нельзя». Попробуем это объяснить.
Напомним, что ошибкой первого рода статистического критерия называется факт принятия альтернативной гипотезы в ситуации, когда верна гипотеза по умолчанию. Например, пусть статистический критерий используется для разграничения доступа к какому-нибудь ресурсу. Тогда отказ в доступе для авторизованного пользователя и будет ошибкой первого рода для такого критерия. Ясно, что возможна «симметричная» ошибочная ситуация, заключающаяся в предоставлении доступа к ресурсу неавторизованному пользователю. Такая ошибка называется ошибкой второго рода: принятие критерием гипотезы по умолчанию в ситуации, когда она неверна (т.е. имеет место альтернативная гипотеза).
Как правило, чувствительность критерия к ошибкам первого рода мы настраиваем самостоятельно (как раз выбором тех самых «стандартных уровней значимости», с которым и сравниваем выдаваемое p-значение). С ошибкой второго рода всё гораздо хуже: её вероятность сильно зависит от выбранной альтернативной гипотезы и является неотъемлемой характеристикой самого критерия. В редких случаях удаётся построить критерий, который является наилучшим (это так называемые равномерно наиболее мощные критерии), и, к сожалению, это невозможно для нашей задачи. В данном случае нулевая гипотеза формулируется просто: выборка имеет нормальное распределение с некоторыми неизвестными параметрами, а альтернативная гипотеза – это полное её отрицание. Альтернативная гипотеза гораздо «богаче» нулевой: в нее входят все распределения, отличные от нормального. Для того и понадобилась целая батарея критериев: одни работают лучше против одного семейства альтернатив, вторые – против другого. Использование всего набора позволяет быть хоть как-то уверенным в том, что распределение, не являющееся нормальным, будет «распознано» хотя бы одним из критериев.
- Критерий Лиллифорса
Критерий Лиллифорса [Lilliefors] является вариантом известного классического критерия Колмогорова–Смирнова, специально модифицированного для проверки нормальности. Эта модификация существенна. Для проверки гипотезы нормальности нельзя использовать классический непараметрический критерий Колмогорова–Смирнова, реализованный в функции ks.test(). Критерий Лиллифорса реализован в функции lillie.test():
> lillie.test(rnorm(100, mean = 6, sd = 4));
Lilliefors (Kolmogorov-Smirnov) normality test
data: rnorm(100, mean = 6, sd = 4)
D = 0.0463, p-value = 0.8621
> lillie.test(runif(100, min = 2, max = 4));
Lilliefors (Kolmogorov-Smirnov) normality test
data: runif(100, min = 2, max = 4)
D = 0.0732, p-value = 0.2089
- Критерии Крамера – фон Мизеса и Андерсона–Дарлинга
Первый критерий известен в русскоязычной литературе под именем критерия ω2 или критерия Смирнова. Эти критерии менее известны, но обычно работают гораздо лучше, нежели критерий Лиллифорса. Они реализованы в функциях cvm.test() и ad.test() соответственно:
> cvm.test(rnorm(50, mean = 6, sd = 4));
Cramer-von Mises normality test
data: rnorm(50, mean = 6, sd = 4)
W = 0.0321, p-value = 0.8123
> ad.test(runif(50, min = 2, max = 4));
Anderson-Darling normality test
data: runif(50, min = 2, max = 4)
A = 1.5753, p-value = 0.0004118
- Критерий Шапиро–Франсиа
Данный критерий работает достаточно хорошо в большинстве не очень «сложных» случаев. Получить p-значение можно посредством функции sf.test():
> sf.test(rexp(50, rate = 2));
Shapiro-Francia normality test
data: rexp(50, rate = 2)
W = 0.7803, p-value = 2.033e-06
- Критерий хи-квадрат Пирсона
В отличие от задач проверки пропорций, критерий хи-квадрат обычно очень плохо работает в задачах проверки распределения на нормальность. Вероятность ошибки второго рода для достаточно широкого класса альтернативных распределений очень велика. В связи с этим, использовать его не рекомендуется.
Тем не менее, его реализация предоставлена функцией pearson.test(). У нее есть булева опция adjusted, которая позволяет внести поправки в p-значение из-за наличия двух неизвестных параметров. Рекомендуемая последовательность действий такая: получить два p-значения: одно – соответствующее adjusted=TRUE, второе – для adjusted=FALSE. Истинное p-значение обычно находится между ними. Кроме того, полезно поварьировать объем выборки и посмотреть, насколько сильно меняется p-значение. Если влияние объёма выборки сильное, то от использования критерия, во избежание ошибок, следует отказаться.
> pearson.test(rnorm(50, mean = 6, sd = 4));
Pearson chi-square normality test
data: rnorm(50, mean = 6, sd = 4)
P = 5.2, p-value = 0.6356
> pearson.test(runif(50, min = -1, max = 1));
Pearson chi-square normality test
data: runif(50, min = -1, max = 1)
P = 7.6, p-value = 0.3692
Теперь мы умеем не только отличать нормальное распределения от «ненормального», но и сравнивать их друг с другом. Это одна из самых первых ступенек на пути понимания сути данных, которые волей-неволей приходится собирать для познания природы абсолютно любых явлений. LXF