- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF104:R
Материал из Linuxformat.
- R Свободный инструментарий для статистической обработки данных
Содержание |
Начала анализа
| R |
|---|
| R на примере |
|---|
- ЧАСТЬ 4 Данные собраны и упакованы – настало время извлечь из них пользу. В конце концов, ведь именно для их анализа вы и поставили R! Алексей Шипунов и Евгений Балдин подскажут пару приемов
Мы не будем останавливаться на том, что такое среднее и как именно вычисляется медиана. Желающие это выяснить могут обратиться за формулами к любому учебнику по статистике.
Начнём с самых элементарных приёмов анализа – вычисления общих характеристик выборки, т.е. набора значений, полученных в результате ряда измерений. Можно сказать, что таких характеристик всего две: центр и разброс. В качестве центральной характеристики чаще всего используются среднее и медиана, а в качестве разброса – стандартное отклонение и квартили. Среднее отличается от медианы прежде всего тем, что оно хорошо работает в случае, если распределение данных близко к нормальному. Медиана не так зависит от характеристики распределения, то есть, как говорят статистики, она более робастна, или устойчива. Понять разницу легче всего на реальном примере. Возьмём опять наших гипотетических сотрудников. Вот их зарплаты (в тыс. руб.):
> salary <- c(21, 19, 27, 11, 102, 25, 21) > names(w) <- c(“Коля”, “Женя”, “Петя”, “Саша”, + “Катя”, “Вася”, “Жора”) > salary Коля Женя Петя Саша Катя Вася Жора 21 19 27 11 102 25 21
Разница в зарплатах может быть обусловлена, например, тем, что Саша – экспедитор, а Катя – глава фирмы. Посмотрим, чему равен центр:
> mean(salary); median(salary) [1] 32.28571 [1] 21
Получается, что из-за высокой Катиной зарплаты среднее гораздо хуже отражает «типичную», центральную зарплату, чем медиана.
Часто ставится задача посчитать среднее (или медиану) для целой таблицы данных. Есть несколько облегчающих жизнь приёмов – проде монстрируем их на примере встроенных данных trees:
> attach(trees) > mean(Girth) [1] 13.24839 > mean(Height) [1] 76 > mean(Volume/Height) [1] 0.3890012 > detach(trees)
Команда attach позволяет присоединить колонки таблицы данных к списку текущих переменных. После этого к переменным можно обращаться по именам, не упоминая имени таблицы. Важно не забыть сделать в конце detach(), потому что велика опасность запутаться в том, что вы присоединили, а что – нет. Кроме того, если присоединённые переменные были как-то модифицированы, на самой таблице это не скажется.
То же самое можно сделать и слегка по-другому:
> with(trees, mean(Volume/Height)) [1] 0.3890012
Этот способ, в сущности, аналогичен первому, только присоединение происходит внутри круглых скобок. Можно также воспользоваться тем фактом, что таблицы данных – это списки колонок:
> lapply(trees, mean) $Girth [1] 13.24839 $Height [1] 76 $Volume [1] 30.17097
Для строк такой прием не сработает, т.е. придется прибегнуть к apply(). Не следует забывать, что циклические конструкции типа for в R использовать не рекомендуется.
Вот как опредяляются стандартное отклонение, варанса (его квадрат) и так называемый межквартильный размах (IQR):
> sd(salary); var(salary); IQR(salary) [1] 31.15934 [1] 970.9048 [1] 6
Опять-таки, IQR лучше подходит для примера с зарплатой, чем стандартное отклонение, и снова – из-за высокой зарплаты у главы фирмы.
> attach(trees) > mean(Height) [1] 76 > median(Height) [1] 76 > sd(Height) [1] 6.371813 > IQR(Height) [1] 8 > detach(trees)
А вот для деревьев эти характеристики куда ближе друг к другу. Разумно предположить, что распределение высоты деревьев близко к нормальному.
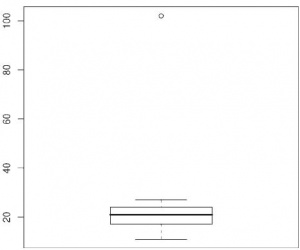
В наших данных по зарплате – всего 7 цифр. Их можно просмотреть глазами и всё понять. А как понять за разумный промежуток времени, есть ли какие-то «выдающиеся» цифры, типа Катиной директорской зарплаты, в данных тысячного размера? Для этого есть графические функции. Самая простая – это так называемый «ящик-с-усами», или «боксплот». Для начала добавим к нашим данным ещё тысячу гипотетических работников с зарплатой, случайно взятой из межквартильного размаха исходных данных:
> new.1000 <- sample((median(salary)-IQR(salary)): + (median(salary)+IQR(salary)), 1000, replace=TRUE) > salary2 <- c(salary, new.1000) > boxplot(salary2)
Это пример интересен ещё и потому, что в нём впервые представлена техника получения случайных значений. Функция sample() способна выбирать случайным образом данные из выборки. В данном случае мы использовали replace=TRUE, поскольку нам нужно было выбрать много чисел из гораздо меньшей выборки. Если писать на R имитацию карточных игр (а такие программы уже написаны!), то надо использовать replace=FALSE, потому что из колоды нельзя достать опять ту же самую карту. Кстати говоря, из того, что значения случайные, следует, что результаты последующих вычислений могут отличаться, если их воспроизвести ещё раз.
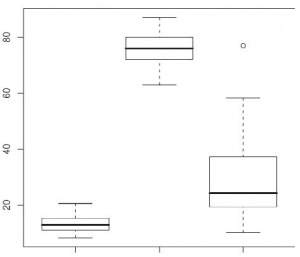
Но вернемся к боксплоту. Как видно из рис. 1, Катина зарплата представлена высоко расположенной точкой. Сам бокс, то есть главный прямоугольник, ограничен сверху и снизу квартилями, так что высота прямоугольника – это IQR. Так называемые «усы» по умолчанию обозначают точки, удалённые на полтора IQR. Линия посередине прямоугольника – это, как легко догадаться, медиана. Точки, лежащие вне усов, рассматриваются как выбросы, и поэтому рисуются отдельно. Боксплоты были специально придуманы известным статистиком Дж. Тьюки [John W. Tukey] (кстати, именно он первый в 1958 г. применил слово software по отношению к программному обеспечению) для того, чтобы быстро, эффективно и устойчиво отражать основные характеристики выборки. R использует оригинальные боксплоты Тьюки, а кроме того, может рисовать несколько боксплотов сразу, то есть эта команда векторизована:
> boxplot(trees)
Есть ещё две функции, которые связаны с боксплотами: функция quantile() по умолчанию выдает все пять квартилей, а функция fivenum() предоставляет все основные характеристики распределения по Тьюки.
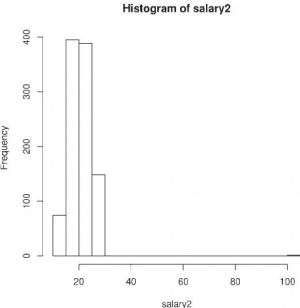
Другой популярный способ изображения выборки (см. рис. 3) – это гистограммы, то есть столбики, высота которых соответствует встречаемости данных, попавших в определенный диапазон:
> hist(salary2, breaks=20)
По умолчанию команда hist разбивает переменную на 10 интервалов, но их количество можно указать и вручную, как в приведенном выше примере (breaks=20). Численным аналогом гистограммы является функция cut(). С её помощью можно выяснить, сколько данных какого типа у нас имеется:
> table(cut(salary2, 20))
(10.9,15.5] (15.5,20] (20,24.6] (24.6,29.1] (29.1,33.7]
74 395 318 219 0
(33.7,38.3] (38.3,42.8] (42.8,47.4] (47.4,51.9] (51.9,56.5]
0 0 0 0 0
(56.5,61.1] (61.1,65.6] (65.6,70.2] (70.2,74.7] (74.7,79.3]
0 0 0 0 0
(79.3,83.9] (83.9,88.4] (88.4,93] (93,97.5] (97.5,102]
0 0 0 0 1
Есть ещё две графические функции, близкие по своей идеологии к гистограмме. В первую очередь это stem() – псевдографическая (текстовая) гистограмма:
> stem(salary, scale=2) The decimal point is 1 digit(s) to the right of the | 1 | 19 2 | 1157 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 2
Логика отображения несложная: значения данных изображаются не точками, а числами, соответствующими самим величинам. Таким образом, видно, что в интервале от 10 до 20 есть две зарплаты (11 и 19), в интервале от 20 до 30 – четыре (21, 21, 25, 27), и т.д.
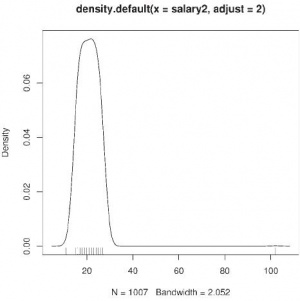
Другая функция тоже близка к гистограмме (см. рис. 4), но требует гораздо более изощрённых вычислений – это график плотности распределения:
> plot(density(salary2, adjust=2)) > rug(salary2)
В этом примере была использована «добавляющая» графическая функция rug(), чтобы акцентировать места с наиболее высокой плотностью. По сути, перед нами сглаживание гистограммы, т.е. попытка превратить её в непрерывную гладкую функцию. Степень сглаживания зависит от параметра adjust (по умолчанию он равен единице).
Ну и, наконец, самая главная функция для описания базовой статистики:
> summary(trees)
Girth Height Volume
Min. : 8.30 Min. :63 Min. : 10.20
1st Qu. : 11.05 1st Qu. :72 1st Qu. : 19.40
Median : 12.90 Median :76 Median : 24.20
Mean : 13.25 Mean :76 Mean : 30.17
3rd Qu. : 15.25 3rd Qu. :80 3rd Qu. : 37.30
Max. : 20.60 Max :87 Max. : 77.00
> lapply(list(salary, salary2), summary)
[[1]]
Min. 1st Qu. Median Mean 3rd Qu. Max.
11.00 20.00 21.00 32.29 26.00 102.00
[[2]]
Min. 1st Qu. Median Mean 3rd Qu. Max.
11.00 17.00 21.00 20.97 24.00 102.00
Заметьте, что у обоих «зарплат» медианы одинаковы, тогда как средние существенно отличаются. Это ещё один пример неустойчивости средних значений, ведь с добавлением случайно взятых «зарплат» вид распределения не должен был существенно поменяться.
Фактически, команда summary() возвращает те же самые данные, что и fivenum(), с добавлением среднего значения (Mean). Однако устроена эта функция более «хитро». Во-первых, она общая, и по законам объекториентированного подхода возвращает разные значения для объектов разного типа. В последнем примере видно, как она работает с числовыми векторами, матрицами и таблицами данных. Для списков она действует по-другому. Вывод может быть таким (на примере встроенных данных о 23 землетрясениях в Калифорнии):
> summary(attenu)
event mag station dist
Min. : 1.00 Min. : 5.000 117 : 5 Min. : 0.50
1st Qu. : 9.00 1st Qu. : 5.300 1028 : 4 1st Qu. : 11.32
Median : 18.00 Median : 6.100 113 : 4 Median : 23.40
Mean : 14.74 Mean : 6.084 112 : 3 Mean : 45.60
3rd Qu. : 20.00 3rd Qu. : 6.600 135 : 3 3rd Qu. : 47.55
Max. : 23.00 Max. : 7.700 (Other) : 147 Max. : 370.00
NA : 16
Переменная station (номер станции наблюдений, третья колонка) – фактор, и к тому же с пропущенными данными. Чтобы не ошибиться, полезно узнать, какие методы существуют у общей функции:
> methods(summary) [1] summary.Date summary.POSIXct [3] summary.POSIXlt summary.aov [5] summary.aovlist summary.connection [7] summary.data.frame summary.default [9] summary.ecdf* summary.factor [11] summary.glm summary.infl [13] summary.lm summary.loess* [15] summary.manova summary.matrix [17] summary.mlm summary.nls* [19] summary.packageStatus* summary.ppr* [21] summary.prcomp* summary.princomp* [23] summary.stepfun summary.stl* [25] summary.table summary.tukeysmooth* Non-visible functions are asterisked
А когда вы запрашиваете помощь, необходимо указать, какая конкретно версия summary() имеется в виду:
> ?summary.data.frame
Одномерные статистические тесты
Закончив разбираться с описательными статистиками, перейдём к простейшим статистическим тестам. Начнём с «одномерных» тестов, которые позволяют проверить утверждения относительно того, как распределены исходные данные.
Предположим, мы считаем, что средняя зарплата в нашем первом примере этой статьи – около 32 тыс. руб. Проверим теперь, насколько эта наша информация достоверна:
> t.test(salary, mu=32)
One Sample t-test
data: salary
t = 0.0243, df = 6, p-value = 0.9814
alternative hypothesis: true mean is not equal to 32
95 percent confidence interval:
3.468127 61.103302
sample estimates:
mean of x
32.28571
Это – вариант теста Стьюдента для одномерных данных. Данный критерий был разработан Уильямом Госсетом [William Sealy Gosset] для оценки качества пива в компании Гиннесс. Статья Госсетт вышла в журнале «Биометрика» под псевдонимом «Student» (cтудент).
Статистические тесты пытаются высчитать т.н. тестовую статистику. Затем на основании этой статистики рассчитывается p-величина (p-value), отражающая вероятность ошибки первого рода. Ошибкой первого рода (или «ложной тревогой»), в свою очередь, называется ситуация, когда мы принимаем альтернативную гипотезу, в то время как на самом деле верна нулевая. Принято считать, что нулевой гипотезе соответствует ситуация «по умолчанию». Наконец, вычисленная p-величина используется для сравнения с заранее заданным порогом (уровнем) значимости. Если p-величина ниже порога, то нулевая гипотеза отвергается, а если выше, то принимается.
Перейдём к анализу вывода функции. Вычисляемая статистика в нашем случае – t (критерий Стьюдента). При шести степенях свободы (df=6, поскольку у нас всего 7 значений) это даёт p-значение, очень близкое к единице (0.9814≈1). Какой бы распространённый порог мы ни приняли (0.1%, 1% или 5%), это значение всё равно больше. Следовательно, мы принимаем нулевую гипотезу (наша информация о средней зарплате скорее верна, чем нет). Поскольку альтернативная гипотеза в нашем случае – это то, что предполагаемое среднее не равно вычисленному среднему, то получается, что «на самом деле» эти цифры статистически не отличаются. Кроме всего этого, функция выдаёт ещё и доверительный интервал (confidence interval), в котором, по её «мнению», может находиться «истинное» среднее. В данном случае он очень широк – от трёх с половиной тысяч до 61 тысячи рублей (это всё из-за высокой Катиной зарплаты).
Существует также непараметрический (не связанный предположениями о распределении) аналог этого теста – ранговый тест Уилкоксона (Wilcoxon signed-rank test):
> wilcox.test(salary2, mu=median(salary2), conf.int=TRUE)
Wilcoxon signed rank test with continuity correction
data: salary2
V = 206882.5, p-value = 0.3704
alternative hypothesis: true location is not equal to 21
95 percent confidence interval:
20.50008 21.00003
sample estimates:
(pseudo)median
20.99995
Эта функция и выводит практически то же самое. Обратите внимание, что тест связан не со средним, а с медианой. Соответственно, вычисляется (если задать conf.int=TRUE) доверительный интервал. Здесь он значительно уже.
Некоторые статистические методы (например, дисперсионный анализ или ANOVA) основаны на том, что данные имеют нормальное распределение. Поэтому вопрос, соответствует ли распределение данных нормальному или хотя бы напоминает ли оно его, является очень и очень важным. В R реализовано несколько разных техник, отвечающих на вопрос о нормальности. Во-первых, это статистические тесты. Самый простой из них – тест Шапиро-Уилка (Shapiro-Wilk test):
> shapiro.test(salary)
Shapiro-Wilk normality test
data: salary
W = 0.6116, p-value = 0.0003726
> shapiro.test(salary2)
Shapiro-Wilk normality test
data: salary2
W = 0.7407, p-value < 2.2e-16
Но что же он показывает? Вывод функции здесь гораздо короче, чем в предыдущих случаях. Более того, даже встроенная справка не содержит объяснений, какая здесь, например, альтернативная гипотеза. Что, собственно, показывает p-значение? Разумеется, можно обратиться к литературе, благо справка даёт ссылки на статьи. А можно просто поставить модельный эксперимент:
> set.seed(1638)
> shapiro.test(rnorm(100))
Shapiro-Wilk normality test
data: rnorm(100)
W = 0.9934, p-value = 0.9094
rnorm() генерирует столько случайных чисел, распределённых по нормальному закону, сколько запрошено через аргумент: это аналог функции sample(). Раз мы получили высокое p-значение, это свидетельствует о том, что альтернативная гипотеза в данном случае: «распределение не соответствует нормальному». Обратите внимание, что для того, чтобы результаты при вторичном воспроизведении были теми же, использована функция set.seed(). Она подстраивает встроенный в R генератор случайных чисел так, чтобы числа в следующей команде были сгенерированы по одному и тому же «закону». Кстати говоря, генераторов случайных чисел в R целых шесть (см. help(set.seed))!
Таким образом, на основании теста Шапиро-Уилка можно заключить, что распределение данных в salary и salary2 существенно отличается от нормального.
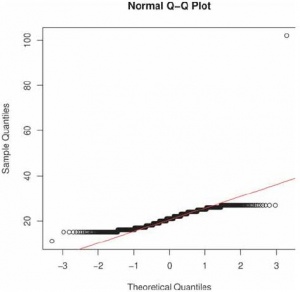
Другой популярный способ проверить, насколько распределение похожее на нормальное – графический (см. рис. 5). Это делается примерно так:
> qqnorm(selary2); qqline(selary2, col=2)
Для каждого элемента вычисляется, какое место он должен занять в сортированных данных (выборочный квантиль), и какое место он должен был бы занять, если бы распределение было нормальным (теоретический квантиль). Прямая проводится через квартили. Если точки лежат на прямой, то распределение нормальное. В нашем случае точки лежат достаточно далеко от красной прямой, а значит, не соответствуют «нормальным».
Как создавать свои функции
Тест Шапиро-Уилка всем хорош, но он не векторизован, как и многие другие тесты в R. Поэтому применить его сразу к нескольким колонкам таблицы данных не получится. Можно, конечно, аккуратно повторить его для каждой колонки, но более глобальный подход – это создать пользовательскую функцию. Например:
> normality <- function(data.f)
+ {
+ result <- data.frame(var=names(data.f),
+ p.value=rep(0, ncol(data.f)),
+ normality=is.numeric(names(data.f)))
+ for (i in 1:ncol(data.f))
+ {
+ data.sh <- shapiro.test(data.f[, i])$p.value
+ result[i, 2] <- round(data.sh, 5)
+ result[i, 3] <- (data.sh > .05)
+ }
+ return(result)
+}
Чтобы функция заработала, надо скопировать эти строчки в окно консоли или записать их в отдельный файл (желательно с расширением .r), а потом загрузить командой source(). После этого её можно вызвать:
> normality(trees)
var p.value normality
1 Girth 0.08893 TRUE
2 Height 0.40342 TRUE
3 Volume 0.00358 FALSE
Функция не только запускает тест Шапиро-Уилка несколько раз, но ещё и аккуратно оформляет результат выполнения. Разберём ее чуть подробнее. В первой строчке указан аргумент data.f. Дальше, в окружении фигурных скобок, находится само тело функции. В третьей строчке формируется пустая таблица данных такой размерности, какая потребуется нам в конце. После этого начинается цикл: для каждой колонки выполняется тест, а потом (это важно!) из теста извлекается p-значение. Эта процедура основана на знании структуры вывода теста – это список, где элемент «p-value» содержит p-значение. Проверить это можно, заглянув в справку, а можно и экспериментально (как? – ищите ответ в конце статьи). Все p-значения извлекаются, округляются, сравниваются с пороговым уровнем значимости (в данном случае – 0.05) и записываются в таблицу. Затем она выдаётся «наружу». Предложенная функция совершенно не оптимизирована. Её легко можно сделать чуть короче, и к тому же несколько «смышлёнее», скажем, так:
> normality2 <- function(data.f, p=.05)
+{
+ nn <- ncol(data.f)
+ result <- data.frame(var=names(data.f),p.value=numeric(nn),
+ normality=logical(nn))
+ for (i in 1:nn)
+ {
+ data.sh <- shapiro.test(data.f[, i])$p.value
+ result[i, 2:3] <- list(round(data.sh, 5), data.sh > p)
+ }
+ return(result)
+}
> normality2(trees)
var p.value normality
1 Girth 0.08893 TRUE
2 Height 0.40342 TRUE
3 Volume 0.00358 FALSE
Результаты, разумеется, не отличаются. Зато теперь видно, как можно добавить аргумент, причём сразу со значением по умолчанию. Теперь можно вызвать функцию чуть по-другому:
> normality2(trees, 0.1)
var p.value normality
1 Girth 0.08893 FALSE
2 Height 0.40341 TRUE
3 Volume 0.00358 FALSE
То есть, если вместо 5 % взять порог в 10 %, то уже и для первой колонки можно отвергнуть нормальное распределение.
Мы не раз говорили, что циклов в R следует избегать. Можно ли сделать это и в данном случае? Оказывается, да:
> lapply(trees, shapiro.test)
$Girth
Shapiro-Wilk normality test
data: X[[1]]
W = 0.9412, p-value = 0.08893
$Height
Shapiro-Wilk normality test
data: X[[2]]
W = 0.9655, p-value = 0.4034
$Volume
Shapiro-Wilk normality test
data: X[[3]]
W = 0.8876, p-value = 0.003579
Как видите, всё ещё проще! Если мы хотим улучшить зрительный эффект для вывода, то можно сделать так:
> lapply(trees, function(.x) + ifelse(shapiro.test(.x)$p.value > .05, + “NORMAL”, “NOT NORMAL”)) $Girth [1] “NORMAL” $Height [1] “NORMAL” $Volume [1] “NOT NORMAL”
Здесь применена так называемая анонимная функция или функция без названия, обычно употребляемая в качестве последнего аргумента команд типа apply(). Кроме того, используется логическая конструкция ifelse(). И, наконец, на этой основе можно сделать третью пользовательскую функцию:
> normality3 <- function(df, p=.05)
+{
+ lapply(df, function(.x)
+ ifelse(shapiro.test(.x)$p.value > p,
+ “NORMAL”,”NOT NORMAL”))
+}
> normality3(list(salary, salary2))
[[1]]
[1] “NOT NORMAL”
[[2]]
[1] “NOT NORMAL”
> normality3(log(trees))
$Girth
[1] “NORMAL”
$Height
[1] “NORMAL”
$Volume
[1] “NORMAL”
Эти примеры тоже интересны. Во-первых, нашу третью функцию можно применять не только к таблицам данных, но и к «настоящим» спискам, с неравной длиной элементов. Во-вторых, простейшее логарифмическое преобразование сразу же изменило «нормальность» колонок. Это следует запомнить, как и то, насколько просто такие преобразования делаются в R. LXF
Ответ на вопроc
> str(shapiro.test(rnorm(100)))