- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF103:R
Материал из Linuxformat.
- R Свободный инструментарий для статистической обработки данных
Содержание |
Типы данных в R и работа с ними
| R |
|---|
| R на примере |
|---|
- ЧАСТЬ 3 Теперь, когда мы уже знаем достаточно для того, чтобы суметь загрузить данные в R, рассмотрим, что же происходит с ними внутри системы, и как, собственно, они обрабатываются.
В статистике, данные принято делить на различные типы, в зависимости от того, насколько близко их можно представить при помощи известной метафоры числовой прямой. Например, возраст человека легко выразить подобным образом, за тем исключением, что он не может быть отрицательным. Размер ботинок представить уже сложнее, поскольку между двумя соседним размерами, как правило, не бывает промежуточного значения, в то время как между двумя любыми числами на числовой прямой всегда можно найти нечто промежуточное. Зато размеры можно хотя бы расположить по возрастающей или по убывающей. А вот c полом человека так уже не получится: есть только два значения, и «промежуточного» просто не бывает. Мы, конечно, можем обозначить женский пол единицей, а мужской – нулем (или двойкой), но никакой числовой информации эти обозначения нести не будут – их даже нельзя отсортировать. Есть ещё и другие специальные виды данных, например, углы, географические координаты, даты и т.п., но все они так или иначе могут быть представлены с помощью чисел. Таким образом, наиболее принципиальное различие между типами данных – возможность или невозможность отобразить их на числа. Если этого сделать нельзя, такие данные принято называть категориальными. Статистические законы, а значит, и статистические программы, работают с этими данными, только если заранее указан их тип. Остальные типы данных в разных книгах называют по разному: числовые, счётные, порядковые или некатегориальные. Мы же примем название «числовые», как самое простое.
Числовые векторы
Допустим, у нас есть данные о росте семи сотрудников небольшой компании. Вот так можно создать из этих данных простейший вектор:
> x <- c(174, 162, 188, 192, 165, 168, 172)
x – это имя объекта R, <- – функция присвоения, c() – функция создания вектора (от англ. «concatenate», собрать). Собственно, R и работает, в основном, с объектами и функциями. У объекта может быть своя структура:
> str(x) num [1:7] 174 162 188 192 165 168 172
то есть x – это числовой (num, numerical) вектор. В других языках программирования бывают ещё скаляры, но в R, как мы знаем (LXF100/101), их нет. «Одиночные» объекты трактуются как векторы из одного элемента.
Вот так можно проверить, вектор ли перед нами:
> is.vector(x) [1] TRUE
Вообще говоря, в R есть множество функций вида is.что-то() для подобной проверки, а ещё есть функции вида as.что-то() – мы будем использовать их далее по тексту. Называть объекты можно, в принципе, как угодно, но лучше придерживаться некоторых простых правил:
- Использовать для названий только латинские буквы, цифры и точку (имена объектов не должны начинаться с точки или цифры);
- Помнить, что R чувствителен к регистру: X и x – это разные имена;
- Не давать объектам имена, уже занятые распространенными функциями (типа c()), а также ключевыми словами (особенно T, F, NA, NaN, Inf).
Для создания «искусственных» векторов очень полезен оператор :, а также функции seq() и rep().
Факторы
Для обозначения категориальных данных в R есть несколько способов, разной степени «правильности». Во-первых, можно создать текстовый (character) вектор:
> sex <- c( “male”, “female”, “male”, “male”, + “female”, “male”, “male”) > is.character(sex) [1] TRUE > is.vector(sex) [1] TRUE > str(sex) chr [1:7] “male” “female” “male” “male” “female” “male” ...
Предположим, что sex – это описание пола сотрудников небольшой организации. Вот как R выводит содержимое этого вектора (Да-да, квадратные скобки – это тоже команда. Можно это проверить, набрав помощь ?”[“):
> sex [1] “male” “female” “male” “male” “female” “male” “male”
Наверное, пора раскрыть загадку единицы в квадратных скобках – это просто номер элемента вектора. Вот как его можно использовать :
> sex[1] [1] “male”
«Умные», то есть объект-ориентированные команды R кое-что «понимают» про объект sex, например, команда table() выводит:
> table(sex)
sex
female male
2 5
А вот команда plot(), увы, не может сделать с таким вектором ничего вразумительного. И это, в общем-то, правильно, потому что программа ничего не знает про свойства пола человека. В таких случаях пользователь сам должен проинформировать R, что его надо рассматривать как категориальный тип данных. Делается это так:
> sex.f <- factor(sex) > sex.f [1] male female male male female male male Levels: female male
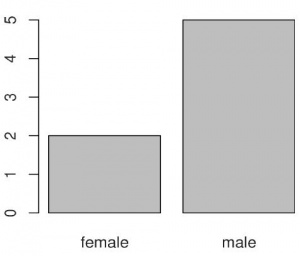
И теперь команда plot() уже понимает, что ей надо делать:
> plot(sex.f)
потому что «видит» специальный тип объекта, предназначенный для категориальных данных – фактор с двумя уровнями (levels):
> is.factor(sex.f) [1] TRUE > is.character(sex.f) [1] FALSE > str(sex.f) Factor w/ 2 levels “female”,“male”: 2 1 2 2 1 2 2
Очень многие функции R (тот же самый plot()) предпочитают факторы текстовым векторам. При этом некоторые умеют конвертировать текстовые векторы в факторы, а некоторые – нет, поэтому надо быть внимательным.
Есть ещё несколько важных свойств факторов, которые надо знать заранее. Во-первых, подмножество фактора – это фактор с тем же количеством уровней, даже если их в подмножестве не осталось:
> sex.f[5:6] [1] female male Levels: female male > sex.f[6:7] [1] male male Levels: female male
«Избавиться» от лишнего уровня можно, только применив специальный аргумент или выполнив преобразование данных «туда и обратно»:
> sex.f[6:7, drop=TRUE] [1] male male Levels: male > factor(as.character(sex.f[6:7])) [1] male male Levels: male
Во-вторых, факторы в отличие от текстовых векторов можно легко преобразовать в числовые значения:
> as.numeric(sex.f) [1] 2 1 2 2 1 2 2
Зачем это нужно, становится понятным, если рассмотреть вот такой пример: положим, кроме роста, у нас есть ещё и данные по весу сотрудников и мы хотим построить такой график, на котором были бы видны одновременно рост, вес и пол. Вот как это можно сделать:
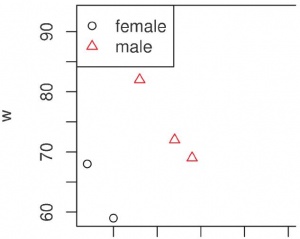
> # Вектор веса > w <- c(69, 68, 93, 87, 59, 82, 72) > # Построение графика > plot(x, w, pch=as.numeric(sex.f), col=as.numeric(sex.f)) > legend( “topleft”, pch=1:2, col=1:2, legend=levels(sex.f))
Тут, разумеется, нужно кое-что объяснить. pch и col – это параметры, предназначенные, соответственно, для определения типа значков и их цвета на графике. Таким образом, в зависимости от того, какому полу принадлежит данная точка, она будет изображена кружком или треугольником и чёрным или красным цветом. При условии, разумеется, что все три вектора соответствуют друг другу. Ещё надо отметить, что изображение пола при помощи значка и цвета избыточно, для «нормального» графика хватит и одного из этих способов.
В-третьих, факторы можно упорядочивать, превращая их некое подобие числовых данных. Введём четвёртую переменную: размер маек для тех же самых гипотетических семерых сотрудников:
> m <- c( “L”, “S”, “XL”, “XXL”, “S”, “M”, “L”) > m.f <- factor(m) > m.f [1] L S XL XXL S M L Levels: L M S XL XXL
Как видно из примера, уровни расположены просто по алфавиту, а нам надо, чтобы S (small) шёл первым. Кроме того, надо как-то сообщить R, что перед нами не просто категориальные, а упорядочиваемые категориальные данные. Делается это так:
> m.o <- ordered(m.f, levels=c( “S”, “M”, “L”, “XL”, “XXL”)) > m.o [1] L S XL XXL S M L Levels: S < M < L < XL < XXL
Теперь R «знает», какой размер больше. Это может сыграть критическую роль, например, при вычислениях коэффициентов корреляции.
Пропущенные данные
В дополнение к векторам из чисел и текстовым векторам, R поддерживает ещё и логические вектора, а также специальные типы данных, которые бывают очень важны для статистических расчётов. Прежде всего это пропущенные или отсутствующие данные, которые обозначаются как NA. Такие данные очень часто возникают в реальных полевых и лабораторных исследованиях, опросах, тестированиях и т.д. При этом следует осознавать, что наличие пропущенных данных вовсе не означает, что данные в целом некачественны. С другой стороны, статистические программы должны как-то с ними работать. Разберём следующий пример: предположим, что у нас имеется результат опроса тех же самых семи сотрудников. Их спрашивали: сколько в среднем часов они спят, при этом один из опрашиваемых отвечать отказался, другой ответил «не знаю», а третьего в момент опроса просто не было в офисе. Так возникли пропущенные данные:
> h <- c(8, 10, NA, NA, 8, NA, 8) >h [1] 8 10 NA NA 8 NA 8
Из примера видно, что NA надо вводить без кавычек, а R нимало не смущается, что среди цифр находится «вроде бы» текст. Отметим, что пропущенные данные очень часто столь же разнородны, как и в нашем примере. Однако кодируются они одинаково, и об этом не нужно забывать.
Tеперь о том, как надо работать с полученным вектором h. Если мы просто попробуем посчитать среднее значение (функция mean()), то получим:
> mean(h) [1] NA
И это «идеологически правильно», поскольку функция может по-разному обрабатывать NA, и по умолчанию она просто сигнализирует о том, что с данными что-то не так. Чтобы высчитать среднее от «не пропущенной» части вектора, можно поступить одним из двух способов:
> mean(h, na.rm=TRUE) [1] 8.5 > mean(na.omit(h)) [1] 8.5
Какой из способов лучше, зависит от ситуации. Часто возникает ещё одна проблема: как сделать подстановку пропущенных данных, скажем, заменить все NA на среднюю по выборке? Распространенное решение примерно следующее:
> h[is.na(h)] <- mean(h, na.rm=TRUE) >h [1] 8.0 10.0 8.5 8.5 8.0 8.5 8.0
В левой части первого выражения осуществляется индексирование, то есть выбор нужных значений h таких, которые являются пропущенными (is.na()). После того, как выражение выполнено, «старые» значения исчезают навсегда.
Матрицы
Матрицы – чрезвычайно распространённая форма представления данных, организованных в форме таблицы. Про матрицы в R, в общем-то, нужно знать две важные вещи: во-первых, что они бывают разной размерности, и во-вторых, что матриц как таковых в R, по сути, нет.
Начнем с последнего. Матрица в R – это просто специальный тип вектора, обладающий некоторыми добавочными свойствами («атрибутами»), позволяющими интерпретировать его как совокупность строк и столбцов. Предположим, мы хотим создать простейшую матрицу 2x2. Для начала воспользуемся числовым вектором:
> m <- 1:4
>m
[1] 1 2 3 4
> ma <- matrix(m, ncol=2, byrow=TRUE)
> ma
[,1] [,2]
[1,] 1 2
[2,] 3 4
> str(ma)
int [1:2, 1:2] 1 3 2 4
> str(m)
int [1:4] 1 2 3 4
Из примера видно, что структура объектов m и ma не слишком различается. Отличен, по сути, лишь их вывод на экран. Сходство между векторами и матрицами прослеживается ещё очевиднее, если создать матрицу несколько иным способом:
> mb <- m
> mb
[1] 1 2 3 4
> attr(mb, “dim”) <- c(2,2)
> mb
[,1] [,2]
[1,] 1 3
[2,] 2 4
Выглядит как некий фокус? Все просто: мы присваивает вектору mb атрибут dim (от слова dimension, т.е. размерность) и устанавливаем значение этого атрибута в c(2,2), то есть две строки и два столбца. Попробуйте догадаться, почему матрица mb отличается от матрицы ma (ответ в конце статьи).
Мы указали лишь два способа создания матриц, а в действительности их гораздо больше. Очень популярно, например, «делать» матрицы из векторов-колонок или строк при помощи команд cbind() или rbind(). Если результат нужно «повернуть» на 90 градусов, используется команда t().
Наиболее распространены матрицы, имеющие два измерения, однако никто не мешает сделать и многомерную матрицу:
> m3 <- 1:8
> dim(m3) <- c(2,2,2)
> m3
,,1
[,1] [,2]
[1,] 1 3
[2,] 2 4
,,2
[,1] [,2]
[1,] 5 7
[2,] 6 8
m3 здесь – это трёхмерная матрица. Естественно, показать в виде таблицы её нельзя, поэтому R выводит её на экран в виде серии таблиц. Аналогично можно создать и четырёхмерную матрицу (как встроенные данные Titanic из предыдущей статьи). Многомерные матрицы в R принято называть «массивами» (arrays).
Списки
Списки – ещё один очень важный тип представления данных. Создавать их, особенно на первых порах, скорее всего, не придется, но знать их особенности необходимо. Это нужно, прежде всего, потому, что очень многие функции в R возвращают именно списки. Для начала знакомства давайте создадим вот такой «тренировочный» список:
> l <- list( “R”, 1:3, TRUE, NA, list( “r”, 4)) >l [[1]] [1] “R” [[2]] [1] 1 2 3 [[3]] [1] TRUE [[4]] [1] NA [[5]] [[5]][[1]] [1] “r” [[5]][[2]] [1] 4
Видно, что список – это своего рода ассорти. Вектор и, соответственно, матрица могут состоять из элементов только одного и того же типа, а вот список – из чего угодно. В том числе, как это видно из примера, и из других списков.
Теперь поговорим про индексирование или выбор элементов списка. Элементы вектора выбираются при помощи функции-квадратной скобки:
> h[3] [1] 8.5
Элементы матрицы выбираются так же, только используется несколько аргументов (для двумерных матриц это номер строки и номер столбца – именно в такой последовательности):
> ma[2, 1] [1] 3
А вот элементы списка выбираются тремя различными методами. Во-первых, можно использовать квадратные скобки:
> l[1] [[1]] [1] “R” > str(l[1]) List of 1 $ : chr “R”
Здесь очень важно, что полученный объект тоже будет списком. Во-вторых, можно использовать двойные квадратные скобки:
> l[[1]] [1] “R” > str(l[[1]]) chr “R”
В этом случае полученный объект будет того типа, какого он был бы до включения в список (так, первый объект будет текстовым вектором, а пятый – списком). В-третьих, можно использовать имена элементов списка. Но для этого сначала надо их присвоить:
> names(l) <- c( “first”, “second”, “third”, + “fourth”, “fifth”) > l$first [1] “R” > str(l$first) chr “R”
Для выбора по имени используется знак $, а полученный объект будет таким же, как при использовании [[]]. На самом деле имена в R могут иметь и элементы вектора, и строки и столбцы матрицы:
> names(w) <- c( “Коля”, “Женя”, “Петя”, “Саша”,
+ “Катя”, “Вася”, “Жора”)
>w
Коля Женя Петя Саша Катя Вася Жора
69 68 93 87 59 82 72
> rownames(ma) <- c( “a1”,”a2”)
> colnames(ma) <- c( “b1”,”b2”)
> ma
b1 b2
a1 1 2
a2 3 4
Единственное условие состоит в том, что все имена должны быть разными. Знак доллара ($) можно использовать только со списками. Отбирать элементы вектора по имени можно так:
> w[ “Женя”] Женя 68
Таблицы данных
Наконец, мы подошли к самому важному типу – таблицам данных (data frames). Именно таблицы данных больше всего похожи на электронные таблицы Excel и аналогов, и поэтому с ними работают чаще всего (это особенно касается начинающих пользователей R). Таблицы данных – это гибридный тип представления, одномерный список из векторов одинаковой длины. Таким образом, каждая таблица данных – это список колонок, причём внутри одной колонки все данные должны быть одного типа. Проиллюстрируем это на примере созданных в этой статье векторов:
> d <- data.frame(weight=w, height=x, size=m.o, sex=sex.f)
>d
weight height size sex
Коля 69 174 L male
Женя 68 162 S female
Петя 93 188 XL male
Саша 87 192 XXL male
Катя 59 165 S female
Вася 82 168 M male
Жора 72 172 L male
> str(d)
'data.frame': 7 obs. of 4 variables:
$ weight: num 69 68 93 87 59 82 72
$ height: num 174 162 188 192 165 168 172
$ size : Ord.factor w/ 5 levels “S”<“M”<“L”<“XL”<“XXL”:
3145123
$ sex : Factor w/ 2 levels “female”,“male”: 2 1 2 2 1 2 2
Поскольку таблица данных является списком, к ней применимы и методы их индексации. Кроме того, таблицы данных можно индексировать и как двумерные матрицы. Вот несколько примеров:
> d$weight [1] 69 68 93 87 59 82 72 > d[[1]] [1] 69 68 93 87 59 82 72 > d[,1] [1] 69 68 93 87 59 82 72 > d[,“weight”] [1] 69 68 93 87 59 82 72
Очень часто бывает нужно отобрать несколько конкретных колонок. Это можно сделать разными способами. Исключим, к примеру, столбец weight:
> d[,2:4]
height size sex
Коля 174 L male
Женя 162 S female
Петя 188 XL male
Саша 192 XXL male
Катя 165 S female
Вася 168 M male
Жора 172 L male
> d[,-1]
height size sex
Коля 174 L male
Женя 162 S female
Петя 188 XL male
Саша 192 XXL male
Катя 165 S female
Вася 168 M male
Жора 172 L male
Второй способ (отрицательная индексация) в некоторых случаях бывает просто незаменим. К индексации имеет прямое отношение ещё один тип данных в R – логические векторы. Как, например, отобрать из нашей таблицы только данные, относящиеся к женщинам? Вот один из способов:
> d[d$sex==“female”,]
weight height size sex
Женя 68 162 S female
Катя 59 165 S female
Чтобы выбрать нужные строки, помещаем перед запятой логическое выражение d$sex==female. Его значением является логический вектор:
> d$sex==”female” [1] FALSE TRUE FALSE FALSE TRUE FALSE FALSE
Таким образом, после того, как «отработает» селекция, в таблице данных останутся только те строки, которые соответствуют значению TRUE, то есть строки 2 и 5.
Более сложным случаем селекции является сортировка таблиц данных. Для сортировки вектора достаточно применить команду sort(), а вот если нужно, скажем, отсортировать наши данные сначала по полу, а потом по росту, приходится действовать более тонко:
> d[order(d$sex, d$height), ]
weight height size sex
Женя 68 162 S female
Катя 59 165 S female
Вася 82 168 M male
Жора 72 172 L male
Коля 69 174 L male
Петя 93 188 XL male
Саша 87 192 XXL male
Команда order() создает не логический, а числовой вектор, который соответствует будущему порядку расположения строк. Подумайте, как применить команду order(), чтобы отсортировать колонки по алфавиту (ответ также можно отыскать в конце статьи).
Векторизованные вычисления
Несмотря на то, что R похож на многие современные скриптовые языки программирования, например, Perl и Python, в нём есть много своеобразного. Одна из интересных и очень полезных особенностей R – это так называемые векторизованные вычисления. Использовать их очень просто. Допустим, мы хотим перевести вес из килограммов в граммы:
> w*1000 Коля Женя Петя Саша Катя Вася Жора 69000 68000 93000 87000 59000 82000 72000
Для такой операции часто требуется использовать циклические конструкции (loops), а здесь всё получается в одно действие. Конечно, в R будут работать и циклы:
> for (i in seq_along(w)) {
+ w[i] <- w[i] * 1000
+}
>w
Коля Женя Петя Саша Катя Вася Жора
69000 68000 93000 87000 59000 82000 72000
но это уж слишком громоздко. Векторизованы и операции между векторами и матрицами:
> ma + mb b1 b2 a1 2 5 a2 5 8 > 1:8 + 1:2 [1] 2 4 4 6 6 8 8 10
В последнем примере второй вектор гораздо короче первого, поэтому при вычислении результата он был несколько раз повторен. Так будет и в том случае, если длина меньшего вектора (матрицы) не кратна длине большего, но тогда R выдаст предупреждение.
Помимо простых арифметических операций, векторизованы и более сложные действия. Существует целое семейство функций, которые специализируются на векторизованных вычислениях: apply(), by(), lapply(), sapply(), tapply() и другие. Вот как работает, например, функция apply():
> apply(trees, 2, mean) Girth Height Volume 13.24839 76.00000 30.17097
Двойка во втором аргументе означает, что среднее (mean()) вычисляется для каждой колонки данных. Для строк надо поставить единицу, но в данном случае это лишено смысла, потому что разные колонки относятся к измерениям разной природы. А вот так при помощи sapply() можно преобразовать наши данные в «кодированный», цифровой вид:
> sapply(d, as.numeric)
weight height size sex
[1,] 69 174 3 2
[2,] 68 162 1 1
[3,] 93 188 4 2
[4,] 87 192 5 2
[5,] 59 165 1 1
[6,] 82 168 2 2
[7,] 72 172 3 2
tapply() и by() позволяют сделать ещё хитрее:
> by(d[,1:2], d$sex, mean) d$sex: female weight height 63.5 163.5 ------------------------------------------------------------ d$sex: male weight height 80.6 178.8
Здесь мы вычислили средний рост и вес для мужчин и женщин за одно действие!
Наконец, lapply() позволяет применить некую команду к каждому элементу списка:
> lapply(d, is.factor) $weight [1] FALSE $height [1] FALSE $size [1] TRUE $sex [1] TRUE
Ответы на вопросы
По ходу статьи мы задали вам пару вопросов – а теперь настало время проверить ответы.
- Ответ на вопрос про матрицы.
Когда мы создавали матрицу ma, мы использовали параметр byrow=TRUE. Значение его по умолчанию – FALSE, и если не задавать его так, как сделали мы, получится точно такая же матрица, как mb.
- Ответ на вопрос про сортировку колонок.
> d[,order(colnames(d))]
В этом случае вместо order() можно было использовать и sort().