- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF110:R
Материал из Linuxformat.
- R Свободный инструментарий для статистической обработки данных
Взаимосвязь случайных величин
| R |
|---|
| R на примере |
|---|
- ЧАСТЬ 2 Сегодня Антон Коробейников и Евгений Балдин сделают тайное явным, вскрыв корреляцию между двумя, казалось бы, совершенно несвязанными событиями, а R им в этом поможет.
Одной из основных задач статистики является изучение зависимостей между данными. При этом слово «зависимость» понимается в самом широком смысле. Скажем, существует однозначная функциональная зависимость, когда, имея только один набор данных, становится возможным полностью определить второй набор. А бывает и другая ситуация: полностью определить второй набор нельзя, но можно попытаться «вытянуть» хоть какую-то информацию о нём.
Корреляция
Начнём всё же с функциональной зависимости, как с наиболее просто формализуемой. Классическим инструментом для измерения линейной зависимости между двумя наборами данных является коэффициент корреляции – числовая величина, находящаяся в интервале от -1 до +1. Чем она больше по модулю (т.е. ближе к +1 или -1), тем выше линейная связь между наборами данных. Знак коэффициента корреляции показывает, в одном ли направлении изменяются эти наборы. Если один из них возрастает, а второй убывает, то коэффициент корреляции отрицателен, а если оба набора возрастают или убывают одновременно – положителен. Значение коэффициента корреляции, равное по модулю 1, соответствует точной линейной зависимости между двумя наборами данных. Линейная же зависимость является самой любимой у экспериментаторов всех мастей.
Обратите внимание, что значение коэффициента корреляции, близкое к нулю, не означает независимости двух наборов данных. Коэффициент корреляции – это мера линейной зависимости, и его равенство нулю означает лишь факт отсутствия последней, но не исключает наличия любой другой. Отсутствие линейной зависимости равносильно независимости только для нормально распределённых выборок, а факт нормальности, естественно, надо проверять отдельно (LXF109).
Для вычисления коэффициента корреляции в R реализована функция cor:
> cor(5:15, 7:17) [1] 1 > cor(5:15, c(7:16, 23)) [1] 0.9375093
В самом простом случае ей передаются два аргумента (векторы одинаковой длины). Кроме того, возможен вызов функции с одним аргументом, в качестве которого может выступать матрица или набор данных (data frame). В этом случае cor вычисляет так называемую корреляционную матрицу, составленную из коэффициентов корреляций между столбцами матрицы или набора данных, взятыми попарно:
> cor(longley)
GNP.deflator GNP Unemployed Armed.Forces
GNP.deflator 1.0000000 0.9915892 0.6206334 0.4647442
GNP 0.9915892 1.0000000 0.6042609 0.4464368
Unemployed 0.6206334 0.6042609 1.0000000 -0.1774206
Armed.Forces 0.4647442 0.4464368 -0.1774206 1.0000000
Population 0.9791634 0.9910901 0.6865515 0.3644163
Year 0.9911492 0.9952735 0.6682566 0.4172451
Employed 0.9708985 0.9835516 0.5024981 0.4573074
Population Year Employed
GNP.deflator 0.9791634 0.9911492 0.9708985
GNP 0.9910901 0.9952735 0.9835516
Unemployed 0.6865515 0.6682566 0.5024981
Armed.Forces 0.3644163 0.4172451 0.4573074
Population 1.0000000 0.9939528 0.9603906
Year 0.9939528 1.0000000 0.9713295
Employed 0.9603906 0.9713295 1.0000000
Если все данные присутствуют, то всё просто; но что делать, когда есть пропущенные наблюдения? Для вычисления корреляционной матрицы в данном случае имеется несколько способов. В команде cor предусмотрена опция use; по умолчанию она равна all.obs, что при наличии хотя бы одного пропущенного наблюдения приводит к ошибке исполнения cor. Если же приравнять use значению complete.obs, то до вычисления корреляционной матрицы из данных удаляются все наблюдения, в которых есть хотя бы один пропуск. Может оказаться так, что пропуски раскиданы по исходному набору данных достаточно хаотично и их много, так что после построчного удаления от матрицы фактически ничего не остаётся. В таком случае поможет попарное удаление пропусков, затрагивающее не всю матрицу сразу, а лишь два столбца непосредственно перед вычислением коэффициента корреляции. Для этого опцию use следует приравнять значению pairwise.complete.obs.
В последнем случае следует принимать во внимание то, что коэффициенты корреляции вычисляются по разному количеству наблюдений, и сравнивать их друг с другом может быть опасно.
> cor(swiss)
Fertility Agriculture Examination
Fertility 1.0000000 0.35307918 -0.6458827
Agriculture 0.3530792 1.00000000 -0.6865422
Examination -0.6458827 -0.68654221 1.0000000
Education -0.6637889 -0.63952252 0.6984153
Catholic 0.4636847 0.40109505 -0.5727418
Infant.Mortality 0.4165560 -0.06085861 -0.1140216
Education Catholic Infant.Mortality
Fertility -0.66378886 0.4636847 0.41655603
Agriculture -0.63952252 0.4010951 -0.06085861
Examination 0.69841530 -0.5727418 -0.11402160
Education 1.00000000 -0.1538589 -0.09932185
Catholic -0.15385892 1.0000000 0.17549591
Infant.Mortality -0.09932185 0.1754959 1.00000000
> # Создаём копию данных.
> swissNA <- swiss
> # Удаляем некоторые данные.
> swissNA[1,2] <- swissNA[7,3] <- swissNA[25,5] <- NA
> cor(swissNA)
Ошибка в cor(swissNA) : пропущенные наблюдения в cov/cor
> cor(swissNA, use = "complete")
Fertility Agriculture Examination
Fertility 1.0000000 0.37821953 -0.6548306
Agriculture 0.3782195 1.00000000 -0.7127078
Examination -0.6548306 -0.71270778 1.0000000
Education -0.6742158 -0.64337782 0.6977691
Catholic 0.4772298 0.40148365 -0.6079436
Infant.Mortality 0.3878150 -0.07168223 -0.1071005
Education Catholic Infant.Mortality
Fertility -0.67421581 0.4772298 0.38781500
Agriculture -0.64337782 0.4014837 -0.07168223
Examination 0.69776906 -0.6079436 -0.10710047
Education 1.00000000 -0.1701445 -0.08343279
Catholic -0.17014449 1.0000000 0.17221594
Infant.Mortality -0.08343279 0.1722159 1.00000000
> cor(swissNA, use = "pairwise")
Fertility Agriculture Examination
Fertility 1.0000000 0.39202893 -0.6531492
Agriculture 0.3920289 1.00000000 -0.7150561
Examination -0.6531492 -0.71505612 1.0000000
Education -0.6637889 -0.65221506 0.6992115
Catholic 0.4723129 0.41520069 -0.6003402
Infant.Mortality 0.4165560 -0.03648427 -0.1143355
Education Catholic Infant.Mortality
Fertility -0.66378886 0.4723129 0.41655603
Agriculture -0.65221506 0.4152007 -0.03648427
Examination 0.69921153 -0.6003402 -0.11433546
Education 1.00000000 -0.1791334 -0.09932185
Catholic -0.17913339 1.0000000 0.18503786
Infant.Mortality -0.09932185 0.1850379 1.00000000
Есть ещё два момента, на которые стоит обратить внимание. Первый – это ранговый коэффициент корреляции Спирмена [Spearman] ρ. Он отражает меру монотонной зависимости и является более робастным (т.е. менее подвержен влиянию случайных «выбросов» в данных). Он бывает полезен в том случае, когда набор данных не получен выборкой из двумерного нормального распределения. Для подсчёта ρ достаточно приравнять опцию method значению spearman:
> x <- rexp(50); > cor(x, log(x), method="spearman") [1] 1
Можно также сравнить, насколько сильно отличаются обычный коэффициент корреляции от коэффициента корреляции Спирмена:
> clP <- cor(longley)
> clS <- cor(longley, method = "spearman")
> i <- lower.tri(clP)
> cor(cbind(P = clP[i], S = clS[i]))
P S
P 1.000000 0.980239
S 0.980239 1.000000
Второй момент – это проверка гипотезы о значимости коэффициента корреляции, что равносильно проверке гипотезы о равенстве его нулю. Если гипотеза отвергается, то влияние одного набора данных на другой считается значимым. Для проверки такой гипотезы используется функция cor.test:
> x <- rnorm(50)
> y <- rnorm(50, mean = 2, sd = 1);
> # Тестируем независимые данные.
> cor.test(x,y)
Pearson's product-moment correlation data: x and y
t = 0.2496, df = 48, p-value = 0.804
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.2447931 0.3112364
sample estimates:
cor
0.03600814
> # Тестируем линейно зависимые данные.
> cor.test(x, 2*x);
Pearson's product-moment correlation
data: x and 2 * x
t = Inf, df = 48, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
11
sample estimates:
cor
1
Видно, что в первом случае гипотеза о равенстве нулю коэффициента корреляции не отвергается, что соответствует исходным данным. Во втором случае вызов был осуществлён с заведомо линейно-зависимыми аргументами, и критерий отвергает гипотезу о равенстве нулю коэффициента корреляции с большим уровнем надёжности. Кроме непосредственно p-значения, функция выводит оценку коэффициента корреляции и доверительный интервал для него. Выставить доверительный уровень можно с помощью опции conf.level. Кроме того, при помощи опции method можно выбирать, относительно какого коэффициента корреляции (простого или рангового) нужно проводить проверку гипотезы значимости.
Следует признать, что смотреть на матрицу, полную чисел, не очень удобно. Поэтому в R есть несколько способов, с помощью которых ее можно визуализировать.
Первый путь – использовать функцию symnum, которая выведет матрицу по-прежнему в текстовом виде, но все числа будут заменены на буквы, в зависимости от того, какому диапазону принадлежало значение:
> symnum(cor(longley))
GNP. GNP U A P Y E
GNP.deflator 1
GNP B 1
Unemployed , , 1
Armed.Forces . . 1
Population B B , . 1
Year B B , . B 1
Employed B B . . B B 1
attr(,"legend")
[1] 0 ‘ ’ 0.3 ‘.’ 0.6 ‘,’ 0.8 ‘+’ 0.9 ‘*’ 0.95 ‘B’ 1}
Функция symnum имеет большое количество разнообразных настроек, но по умолчанию они все выставлены в значения, оптимальные для отображения корреляционных матриц.
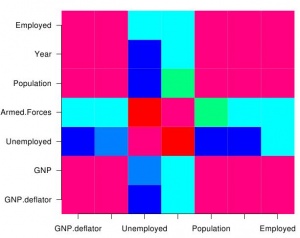
Второй способ – «настоящее» графическое представление корреляционных коэффициентов. Идея проста: нужно разбить область от -1 до +1 на отдельные диапазоны, назначить каждому из них свой цвет, а затем вывести всё это на экран (рис.1). Для этого следует воспользоваться функциями image и axis:
> C <- cor(longley) > image(1:ncol(C), 1:nrow(C), C, col = rainbow(12),
+ axes = FALSE, xlab = "", ylab = "")
> # Подписи к осям. > axis(1, at = 1:ncol(C), labels=colnames(C)) > axis(2, at = 1:nrow(C), labels=rownames(C), las = 2)
Ещё один интересный способ представления корреляционной матрицы реализуется пакетом ellipse. В данном случае значения коэффициентов корреляции рисуются в виде эллипсов, отражающих форму плотности двумерного нормального распределения с данным значением корреляции между компонентами. Чем ближе значение коэффициента корреляции к +1 или -1, тем более вытянутым становится эллипс. Наклон эллипса отражает знак коэффициента. Для получения изображения необходимо вызвать функцию plotcorr (рис.2):
> # Устанавливаем библиотеку. > install.packages(pkgs=c(«ellipse»)) > # Загружаем. > library(ellipse) > # Используем. > plotcorr(cor(longley))
Таблицы сопряжённости
Таблицы сопряжённости (contigency tables) – это удобный способ изображения категориальных переменных и исследования зависимостей между ними. Они представляют собой таблицы, ячейки которых индексируются градациями участвующих факторов, а их содержимое равняется количеству наблюдений с данными градациями. Построить таблицу сопряжённости можно с помощью функции table. В качестве аргументов ей нужно передать факторы, на основе которых будет строиться таблица сопряжённости:
> # Таблица сопряжённости для выборки, имеющей
> # распределение Пуассона (n=100, λ=5).
> table(rpois(100,5))
0 2 3 4 5 6 7 8 9 10 11
1 7 18 17 22 13 13 4 1 1 3
> with(airquality, table(cut(Temp, quantile(Temp)), Month))
Month
5 6 7 8 9
(56,72] 24 3 0 1 10
(72,79] 5 15 2 9 10
(79,85] 1 7 19 7 5
(85,97] 0 5 10 14 5
R использует «честное» представление для трёх- и более мерных таблиц сопряжённости, то есть каждый фактор получает по своему измерению. Однако это не очень удобно при выводе подобных таблиц на печать или сравнении с имеющимися в литературе. Традиционно для этого применяются «плоские» таблицы сопряжённости, когда все факторы, кроме одного, объединяются в один «многомерный» фактор, градации которого и используются при построении таблицы сопряжённости. Построить плоскую таблицу сопряжённости можно с помощью функцией ftable:
> ftable(Titanic, row.vars = 1:3)
Survived No Yes
Class Sex Age
1st Male Child 0 5
Adult 118 57
Female Child 0 1
Adult 4 140
2nd Male Child 0 11
Adult 154 14
Female Child 0 13
Adult 13 80
3rd Male Child 35 13
Adult 387 75
Female Child 17 14
Adult 89 76
Crew Male Child 0 0
Adult 670 192
Female Child 0 0
Adult 3 20
Опция row.vars позволяет указать номера переменных в наборе данных, которые следует объединить в один фактор, градации которого будут индексировать строки таблицы сопряжённости. Опция col.vars проделывает то же самое, но для столбцов таблицы.
Функцию table можно использовать и для других целей. Самое простое – это подсчёт частот. Например, можно считать пропуски:
> d <- factor(rep(c("A","B","C"), 10), levels=c("A","B","C","D","E"))
> is.na(d) <- 3:4
> table(factor(d, exclude = NULL))
A B C <NA>
9 10 9 2
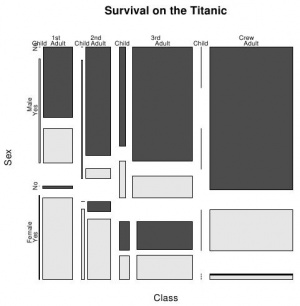
Функция mosaicplot (рис. 3) позволяет получить графическое изображение таблицы сопряжённости (именно она вызывается, когда вы передаете таблицу сопряжённости стандартной функции plot):
> mosaicplot(Titanic,main="Survival on the Titanic",color=TRUE)
При помощи функции chisq.test можно проверить гипотезу о независимости двух факторов (того же эффекта можно добиться, если передать таблицу сопряжённости в качестве аргумента функции summary). Например, проверим гипотезу о независимости цвета глаз и волос:
> x <- margin.table(HairEyeColor, c(1, 2))
> chisq.test(x)
Pearson's Chi-squared test
data: x
X-squared = 138.2898, df = 9, p-value < 2.2e-16
Набор данных HairEyeColor – это многомерная таблица сопряжённости. Здесь для суммирования частот по всем, кроме двух, «измерений» использовалась функция margin.table. Таким образом в результате была получена двумерная таблица сопряжённости.
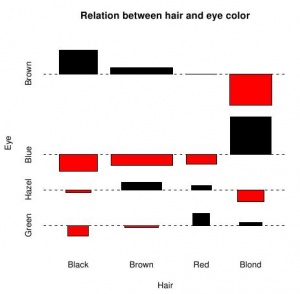
При желании изобразить зависимости между градациями двух факторов графически можно воспользоваться функцией assocplot. На рис. 4 показаны отклонения ожидаемых (при предположении независимости факторов) частот от наблюдаемых величин. Высота прямоугольника показывает абсолютную величину этого отклонения, а положение – его знак. Ширина прямоугольника отображает собственно саму ожидаемую величину значения в ячейке, но она не так информативна для предварительного анализа.
> x <- margin.table(HairEyeColor, c(1, 2)) > assocplot(x, main = "Relation between hair and eye color")
Нетрудно видеть, что для людей со светлыми волосами характерен голубой цвет глаз и совсем не характерен карий, а для обладателей чёрных волос ситуация в точности обратная.
Поиск зависимостей между различными наборами данных – любимое занятие человека разумного. Обнаружение новой, ранее неизвестной, зависимости – одно из самых больших интеллектуальных удовольствий. Вдвойне приятно, если эта зависимость получается линейной. LXF