Материал из Linuxformat.

GLSL Проникаем в тайны видеоускорителя с программами на шейдерах.

Игрострой: Ни строчки кода!
Часть 1: Ни строчки кода! Часть 2: Система управления Часть 3: Добавим текстуры Часть 4: Меню

Игрострой: Шейдеры
Часть 1: Нереальная реальность Часть 2: Текстуры на заказ Часть 3: Да будет свет!

Содержание 1 Текстуры на заказ 1.1 Джек, который построил дом... 1.2 Noise-фактор 1.3 Под фанеру

Текстуры на заказ

ЧАСТЬ 2 Оказывается, текстуры можно создавать не только в графическом редакторе! Андрей Прахов умеет делать это на лету, при помощи… правильно, программ-шейдеров.

Когда-то, много лет назад, я увлекался программированием на ассемблере для микрокомпьютера ZX-Spectrum. В наше время его технические характеристики могут вызвать разве что улыбку: ОЗУ 48-1024 КБ, процессор 3,4 МГц. Однако, несмотря на крохотную память, малые тактовые частоты и полное отсутствие какого-либо ускорения графики, на нем делались потрясающие игры и демо. Существовало повальное увлечение демо-сценой, когда программист старался вместить музыку, графику, спецэффекты в ничтожное количество байт. Современные игры пожирают гигабайты места на винчестере и многие мегабайты простой и видеопамяти. Откуда такие аппетиты? Наиболее ресурсоемкие части игры – это графика и музыка. Особенно трудно приходится программистам при расчете объема текстурной памяти, необходимого для определенного момента текущей сцены. Уменьшить объем используемой видеопамяти можно, если заменить обычные текстуры процедурными, то есть вычисляемыми в нужный момент времени. В этом случае ОЗУ расходуется только на генерирующую программу. Понятное дело, это требует немалых вычислительных мощностей, если не поручить ее выполнение GPU, а точнее – его шейдерным конвейерам.

Специально для этого урока я подготовил модель дома с окружением, но вот основные текстуры для него мы заменим на процедурные программы. Итак, нам предстоит разработать шейдеры для основания дома, стен, окон и двери, т.е. создать имитации мрамора, дерева и кирпича. Давайте прикинем, сколько же мы на этом сэкономим? Если брать за стандарт текстуру формата Targa с разрешением 1024х1024, то в сумме получится... ого, примерно шесть мегабайт! За них стоит побороться.

Джек, который построил дом...

Вначале определимся с вершинным шейдером, который будет одинаковым для всех примеров. Возьмем за основу код вычисления диффузного освещения из предыдущего урока и немного переделаем его:

//GLSL vertex shader
void main ()
const vec4 inColor = vec4 (1.0, 0.0, 0.0, 1.0);
uniform vec3 lightPos;
  varying vec4 outColor;
  {
            vec3 position = vec3 (gl_ModelViewMatrix * gl_Vertex);
            vec3 lightvec = normalize (vec3 (lightPos) - position);
            vec3 norm = normalize (gl_NormalMatrix * gl_Normal);
            outColor = inColor * (max (dot (norm, lightvec), 0.0));
            gl_Position = gl_ModelViewProectionMatrix * gl_Vertex;
            gl_Position = ftransform();
  }

В приведенном выше примере мы передавали координаты источника света через переменную LightPos. На этом уроке будет удобнее брать их непосредственно из самого шейдера. Раз у нас всего один источник света, то строка будет выглядеть следующим образом:

vec3 ll=gl_LightSource[0].position;

Так как основные манипуляции будут происходить во фрагментном шейдере, то логичнее было бы вычислять не полное освещение и цвет текущей вершины, а всего лишь интенсивность светового потока. В приведенном коде за это отвечает строка

outColor = inColor * (max (dot (norm, lightvec), 0.0));

Здесь происходит умножение постоянного цвета примитива (переменная InColor) на интенсивность освещения. Соответственно, удалив первый операнд, мы получим необходимый код. Заодно поменяем название выходной varying-переменной на более подходящее имя outLight. В дальнейшем останется только умножить результат работы фрагментного шейдера на outLight для получения конечного результата. Кроме того, для работы нам понадобятся координаты рассчитываемой вершины. Введем для этого новую переменную MCposition. Реализация последней задачи будет немного варьироваться для каждого конкретного шейдера, и мы обговорим ее отдельно.

Со всеми приведенными изменениями у нас получился следующий код вершинного шейдера:

//GLSL vertex shader (optimization for break)
void main ()
varying float outLight;
varying vec2 MCposition;
{
            vec3 ll=gl_LightSource[0].position;
            vec3 position = vec3 (gl_ModelViewMatrix * gl_Vertex);
            vec3 lightvec = normalize (vec3 (ll) – position);
            vec3 norm = normalize (gl_NormalMatrix * gl_Normal);
            outLight = max (dot (norm, lightvec), 0.0);
            gl_Position = gl_ModelViewProectionMatrix * gl_Vertex;
            MCposition = gl_Vertex.xy;
}

Существуют два варианта создания процедурной текстуры: использование особого алгоритма для повторяющихся элементов рисунка и работа с шумовыми функциями. Сначала мы разработаем шейдер для имитации кирпичной стены. В этом случае наиболее естественным выглядит первый вариант.

Создаваемая нами программа должна учитывать следующие особенности:

• Кирпичная кладка состоит из блоков одинакового размера, где каждый кирпич отделен друг от друга пространством другого цвета;
• Каждый следующий ряд сдвинут по отношению к предыдущему на половину длины кирпича.

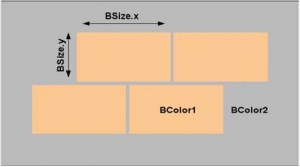
Давайте определимся с необходимыми переменными. Это uniform-переменные для хранения цветов самих кирпичей и промежутков между ними. Кроме того, нам еще понадобятся размеры брусков с учетом имеющихся промежутков и процентное соотношение общих размеров с реальными размерами кирпича (рис. 1). Итого получается четыре переменные:

  uniform vec3 BColor1, Bcolor2; // (1.0,0.4,0.0), (1.0,1.0,1.0)
  uniform vec2 Bsize, BP; // (0.30,0.15), (0.90,0.85)

Чтобы определить, к какой точке объекта принадлежит текущий фрагмент, нам необходимо передать в varying-переменной координаты рассчитываемой вершины. Для этого в vertex-шейдере служит строка

MCposition = gl_Vertex.xy;

Таким образом мы также удалим нежелательный эффект скольжения рисунка. Не забудьте разместить эту переменную в обоих шейдерах!

Теперь нам нужно определить, как рисовать текущий ряд кирпичиков: ведь каждый второй у нас идет со смещением. Однако вначале необходимо вычислить номера ряда и блока в нем. Простым делением координат вершины на размер кирпича мы получим ряд в переменной Lpos.y и номер блока в Lpos.x:

vec2 Lpos = MCposition / Bsize;

А вот теперь самое интересное! Для определения смещения мы воспользуемся оператором ветвления IF...ELSE. Замечу, что правила написания его абсолютно аналогичны таковым в C/C++. Так как у нас кирпич должен смещаться на 0.5 от своей длины, то для расчета мы возьмем номер ряда из переменной Lpos.y, умножим его на 0.5 и отбросим функцией fract целую часть результата. Полученный результат сравнивается с 0.5. Таким образом, через раз условие будет истинным, а ряд – смещаться на 0.5:

if (fract (Lpos.y * 0.5)>0.5) Lpos.x +=0.5;

Для выбора цвета на текущем участке необходима функция, возвращающая 1 на кирпиче и 0 на промежутке. Их у нас будет две, ведь существуют и горизонтальные, и вертикальные компоненты. Результаты обеих функций перемножаются для получения окончательного цвета.

И снова на помощь нам приходит мощь языка GLSL в виде уже готовой функции step (edge, x). Вообще-то она служит для получения импульсов прямоугольной формы. В нашем случае, функция будет возвращать 0 при условии BP.x <= Lpos.x и единицу в случае несоответствия. Однако вначале следует вычислить координаты фрагмента по отношению к активному блоку:

Lpos = fract (Lpos);
vec2 uses = step (Lpos, BP);

Дело осталось за малым – надо вычислить окончательное значение цвета и умножить его на переменную outLight для получения правильного освещения фрагмента. Воспользуемся встроенной функцией mix (vec4 x, vec4 y, float a). Ее воплощение выражается формулой x*(1.0-a)+y*a. Так как результат операции uses.x * uses.y может принять либо единицу, либо ноль, то и функция будет возвращать одно-единственное значение (при 1 – цвет кирпича, при 0 – цвет промежутка).

Конечный код фрагментного шейдера кирпичной стены (рис. 2) таков:

//GLSL fragment shader
uniform vec3 BColor1, BColor2;
uniform vec2 BSize, BP;
varying vec2 MCposition;
varying float outLight;
void main() {
       vec2 Lpos = MCposition / BSize;
       if (fract (Lpos.y * 0.5)>0.5)
              Lpos.x +=0.5;
       Lpos = fract (Lpos);
       vec2 uses = step (Lpos, BP);
       vec3 color = mix (BColor2, BColor1, uses.x * uses.y) * outLight;
               gl_FragColor = vec4 (color, 1.0);
}

Noise-фактор

Зачастую при упоминании термина «шум» у непосвященных возникает ассоциация либо со звуком, либо с отсутствием сигнала на телеэкране (хаотичный «снег»). Однако в трехмерной графике использование «чистого» шума не имеет смысла. Ведь, как правило, текстура при наложении на объект размножается, и в случае «чистого» шума добиться необходимого узора невозможно. Шумовые функции выдают непрерывную псевдослучайную последовательность, которая зависит от начального значения. Благодаря этим особенностям появляется возможность имитации цветов природных и искусственных материалов, неровностей поверхностей, «хаотичной» анимации.

В случае с шейдерами предлагается три способа работы с шумом:

• Использование встроенных функций GLSL;
• Текстурные карты;
• Функции, определяемые пользователями.

Язык программирования шейдеров имеет встроенную процедуру для генерации шумов – noise(). Использование этого подхода имеет ряд преимуществ по сравнению с остальными. Во-первых, не расходуется текстурная память на хранение карты шумов. Кроме того, шейдеры, использующие noise(), не зависят от конкретного приложения. Однако в наше время эта функция, как правило, не применяется из-за неполной аппаратной реализации. Гораздо проще и быстрее один раз вычислить необходимую последовательность и сохранить ее в текстурной карте. В каждой текстуре можно хранить до 4 различных значений и получать их за одно обращение. Данные разделяются и хранятся в каналах RGBA. Замечу, что могут использоваться не только двумерные, но и трех-, четырехмерные карты шумов. В нашем случае, мы будем работать с двумерной, уже заранее просчитанной картой. Что же касается процедуры генерации, то ее легко написать самому или воспользоваться всезнающим Интернетом. Здесь при создании карты шумов использовалась стандартная функция Перлина.

Попробуем для начала смоделировать узор, напоминающий мраморный камень. Исправьте вершинный шейдер, заменив в нем строку:

MCposition = gl_Vertex.xy;

на

MCposition = vec3 (gl_Vertex);

То есть, в отличие от первого шейдера, мы будем использовать полноценные трехмерные координаты вершины. Не забудьте при этом изменить описание переменной в начале программы. На этом модификация вершинного шейдера завершена.

Для фрагментного шейдера нам понадобятся следующие переменные:

uniform sampler2D NoiseMap;
uniform vec3 MColor1; //0.80,0.86,0.74
uniform vec3 MColor2; //0.35,0.15,0.1

где MColor1 хранит основной цвет камня, а MColor2 – цвет прожилок. Кроме того, шейдеру необходимо указать на текстурную карту, которая будет использоваться для генерации шума. За это отвечает строка

 uniform sampler2D NoiseMap.

Решение задачи донельзя простое. Загружаем в вектор значения шума с шагом 1.5 для активного пикселя:

vec3 noisevec = texture2D (NoiseMap, MCposition *1.5);

Вычисляем интенсивность узора путем сложения обоих векторов:

float intensity = (noisevec[0] - 0.5) +(noisevec[1] - 0.25);

Для создания прожилок воспользуемся функцией sin (float x):

float ssin = sin(MCposition.y * 100.0 + intensity * 100.0)+0.4;

Осталось вычислить конечный цвет способом, который мы уже использовали для шейдера кирпичной стены. Но слишком уж это скучно! Давайте усложним задачу, разбив мрамор на некое подобие плиток. Чтобы не изобретать велосипед, воспользуемся готовым шейдером кирпича с небольшими модификациями.

Конечный результат работы программы должен отвечать следующим требованиям:

• Поверхность модели разбита на квадраты, напоминающие шахматную доску;
• Узор мрамора непрерывен и неразрывен для всей площади объекта.

Исходя из поставленных условий, логичнее всего произвести разбивку на квадраты, а потом залить все узором мрамора. За рисунок кирпичей у нас отвечали строки

if (fract (Lpos.y * 0.5)>0.5)
             Lpos.x +=0.5;
Lpos = fract (Lpos);
vec2 uses = step (Lpos, BP);

Опытным путем несложно добиться, чтобы небольшая модификация кода привела к желаемому результату:

if (fract (Lpos.y )>0.5)
             Lpos.x +=0.5;
Lpos = fract (Lpos);
vec2 uses = step (Lpos, BP);

Однако результат выбора цвета необходимо занести в отдельную переменную и обобщить только после вычисления кода «мрамора». Конечный код фрагментного шейдера мраморных плиток выглядит следующим образом:

//GLSL fragment shader
uniform sampler2D NoiseMap;
uniform vec3 MColor1;
uniform vec3 MColor2;
uniform vec3 BColor1, Bcolor2; //0.0,0.0,0.0 | 0.5,0.5,0.5
uniform vec2 BSize, BP; //1.30,1.15 | 0.50,1.0
varying float outLight;
varying vec3 MCposition;
void main ()
{
             // вычисляем квадраты
vec2 Lpos = MCposition / BSize;
if (fract (Lpos.y )>0.5)
             Lpos.x +=0.5;
Lpos = fract (Lpos);
vec2 uses = step (Lpos, BP);
vec3 color1 = mix (BColor2, BColor1, uses.x * uses.y);
// генерируем узор
vec3 noisevec = texture2D (NoiseMap, MCposition *1.5);
float intensity = (noisevec[0] - 0.5) +(noisevec[1] - 0.25);
float ssin = sin(MCposition.y * 100.0 + intensity * 100.0)+0.4;
// перемешиваем и загружаем в gl_FragColor
vec3 color = mix(MColor2+color1, MColor1+color1, ssin) * outLight;
gl_FragColor = vec4 (color, 1.0);
}

У полученного шейдера немало недостатков, однако со своей ознакомительной функцией он вполне справляется (рис. 3). Если еще немного поиграть с параметрами, можно добиться гораздо более естественного результата, но нас ждет последний в этом уроке шейдер деревянной поверхности.

Под фанеру

Принцип его создания примерно такой же, как и в случае с мрамором. Уточним условия задачи:

• Рисунок поверхности состоит из чередования светлых и темных участков в форме концентрических цилиндров;
• Для реалистичности необходимо искажение цилиндров при помощи шума.

Для шейдера деревянной поверхности нам понадобятся переменные, содержащие основной и дополнительный цвета, масштабирование и фактор искажения для создания шума:

uniform vec3 LWood; //0.9,0.8,0.6
uniform vec3 DWood; //0.6,0.3,0.04
uniform vec3 NScale; //0.1,0.1,0.1
uniform float NNess; //3.0

Как обычно, вначале загружаем в вектор карту шумов и настраиваем необходимый тип генерации:

vec3 noisevec = vec3 (texture2D (NoiseMap, MCposition * NScale)*Nness);

Последние два параметра отвечают за толщину и узор волокон. Поиграйте с ними и посмотрите, что получится. Мы высчитываем конечные координаты в соответствии с полученным вектором и координатами вершины:

vec3 location = MCposition + noisevec;

Теперь займемся рисованием кругов. Для этого нужно знать расстояние от оси бревна до текущего годичного кольца. Возведем координаты x и z в квадрат и извлечем из них квадратный корень. Количество кругов можно контролировать, если перемножить коэффициент масштабирования на полученный результат:

float dist = sqrt (location.x * location.x * location.z * location.z);
dist *=4;

Однако то, что у нас сейчас получилось, очень мало напоминает дерево. Обычно структура древесины не состоит из строгих концентрических цилиндров с резким разделением на темные и светлые полосы, а имеет плавные переходы между ними. Добиться этого можно, если написать функцию с постепенным изменением значения от 0 до 1.0 и наоборот. Необходимо сложить полученное расстояние с тремя октавами шума и выделить из результата дробную часть. Небольшой кусок кода будет отвечать за своевременное изменение конечного значения:

float r = fract (dist + noisevec[0] + noisevec [1] + noisevec[2]);
if (r > 1.0) r = 2.0 -r;

Вот таким образом мы получили необходимые данные для функции mix на выходе. Остальной код вам хорошо знаком. В целом, фрагментный шейдер дерева выглядит следующим образом (рис. 4):

//GLSL fragment shader (wood)
uniform sampler2D NoiseMap;
uniform vec3 LWood;
uniform vec3 DWood;
uniform vec3 NScale;
uniform float NNess;
varying float outLight;
varying vec3 MCposition;
void main ()
{
      vec3 noisevec = vec3 (texture2D (NoiseMap, MCposition * NScale)* NNess);
       vec3 location = MCposition + noisevec;
      float dist = sqrt (location.x * location.x * location.z * location.z);
       dist *=4;
      float r = fract (dist + noisevec[0] + noisevec [1] + noisevec[2]);
      if (r > 1.0)
                   r = 2.0 -r;
      vec3 color = mix (LWood, DWood, r);
      color *= outLight;
      gl_FragColor = vec4 (color, 1.0);
}

Процедурные текстуры занимают немаловажное место в реалистичной визуализации сцены. Они компактны, шустры и очень гибки в плане настраиваемости под конкретную задачу. Но даже если откинуть нарочитость простоты реализации наших шейдеров, видно, что до уровня естественности они явно не дотягивают. Большое значение при этом имеет правильная работа с освещением. Именно этому будет посвящен следующий урок. LXF