- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF82:PAW
Материал из Linuxformat.
| Анализ данных |
|---|
|
Содержание |
PAW: приемы работы
ЧАСТЬ 2 Впечатлены возможностями PAW? Приготовьтесь к большему — сейчас Евгений Балдин продемонстрирует вам эту систему в деле!
Система анализа данных PAW или Physics Analysis Workstation для своей работы не требует доскональных знаний всех подсистем и команд. Но чтобы действовать эффективно, следует изучить логику построения команд и стандартные приемы. Это позволит в дальнейшем легко получать навыки для выполнения более сложных задач.
Если даже вы не планируете использовать PAW, в любом случае будет полезно присмотреться к этому инструменту, так как он сравнительно прост и основные концепции, необходимые для анализа данных, достаточно прозрачны для понимания. Создатели PAW действовали по принципу минимализма. Делалось только необходимое — никаких «рюшечек», зато просто. Жесткая структура команд дополнена возможностью писать свои функции и скрипты.
Простейший анализ
Учиться лучше всего на примере реального анализа. Попробуем сделать нечто подобное.
Будем считать, что программа PAW уже запущена и мы находимся в рабочей директории. Вызов внешних команд обеспечивается с помощью инструкции SHELL (можно сократить до sh).
PAW > sh ls ascii.png lkravg.dat PAW.metafile ee-ang.rz th1.eps last.kumac last.kumacold sin.dat
Необходимо провести предварительный анализ данных, представленных в текстовом файле lkravg.dat:
1099279655 4119 0.8318 0.0014 1.13 5.99195 1099397693 4126 0.8404 0.0032 1.07 6.001685 …
Колонки соответствуют time_t — времени в секундах, номеру измерения, исследуемому значению, ошибке значения для текущего измерения и двум сторонним параметрам, от которых интересующее нас значение может зависеть. Задача: имея время и два сторонних параметра, попробовать предсказать исследуемое значение.
Анализировать можно и без модели явления, но чтобы правильно подготовить данные для исследования, необходимо ее иметь. Легенда для этих данных следующая: исследуемое значение представляет из себя степень «ухудшения» качества жидкого криптона (LKr — Liquid Kripton) в LKr-калориметре для регистрации энергии элементарных частиц. Качество вычисляется в относительных единицах по амплитуде сигнала от космических мюонов (эти частицы хорошо выделяются и есть всегда). Два параметра, от которых может зависеть качество: избыточное давление LKr и магнитное поле, в котором находится калориметр. Избыточное давление примерно линейно связано с температурой LKr, что влияет на амплитуду сигнала. В магнитном поле прямолинейная траектория мюона искажается, что тоже может влиять на амплитуду.
В первую очередь, необходимо прочитать данные из текстового файла. Для этого можно воспользоваться командой VECTOR/READ (help ve/re):
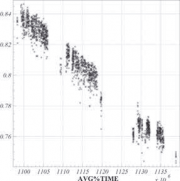
#чтение текстового файла в вектора PAW > ve/re time,run,avg,avg_er,P,H lkravg.dat # меняем тип маркера PAW > set mtyp 2 # изобразим зависимость исследуемого значения от времени PAW > ve/pl avg%time
Из рисунка ниже видно, что исследуемое значение в среднем уменьшается за большой промежуток времени (исследуемый интервал равен году и четырем месяцам), и в то же время у данных есть структура, соответствующая более короткому интервалу.
Сначала исключим временную зависимость. Воспользуемся для этого стандартной процедурой подгонки для векторов VECTOR/FIT X Y EY FUNC (help ve/fit), где X соответствует оси времени, Y — исследуемому значению, EY — ошибки определения значения, а FUNC — подгоночной функции. Вместо FUNC можно передать любую функцию, написанную на FORTRAN, но в нашем случае достаточно полинома первой степени. Для полинома в PAW есть сокращенное обозначение PN, где N - степень полинома.
#подгоняем временную зависимость прямой PAW > ve/fit time avg avg_er P1 ********************************************************* * * * Function minimization by SUBROUTINE HFITV * * Variable-metric method * * ID = 0 CHOPT = * * * ********************************************************* Convergence when estimated distance to minimum (EDM) .LT. 0.10E+01 EXT PARAMETER APPROXIMATE STEP FIRST NO. NAME VALUE ERROR SIZE DERIVATIVE 1 P1 3.3620 0.50070E-03 0.85051E-02 -223.19 2 P2 -0.22939E-08 0.44872E-12 0.58032E-11 -0.27325E+12 CHISQUARE = 0.1680E+02 NPFIT = 1644
При выполнении процедуры подгонки PAW выдает стандартную «портянку». Основной интерес для пользователя представляют результаты подгонки. В случае полинома первой степени подгоняются два параметра P1 — свободная константа и P2 — коэффициент пропорциональности
Для исключения временной зависимости воспользуемся пакетом SIGMA (help sigma). С помощью команды sigma векторами можно манипулировать, как обычными переменными:
#создаем новый вектор уже без временной зависимости PAW > sigma avg1=avg-3.3620+0.22939E-08*time
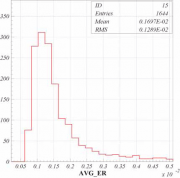
Прежде чем действовать дальше, оценим, какую точность в принципе можно ожидать. Вектору исследуемой величины avg соответствует вектор ошибок avg_er. Посмотрим, чему равны эти ошибки. Число измерений превосходит полторы тысячи, поэтому просмотреть все значения глазами не очень реально. Лучше создать гистограмму:
#создаем из значений вектора гистограмму N15 PAW > ve/pl avg_er 15 #включаем отображение статистики (число событий/среднее/разброс) PAW > opt sta #меняем цвет гистограммы на красный PAW > set hcol 2 #вывод гистограммы N15 в диапазоне от 0. до 0.01 PAW > hi/plot 15(0.:0.01)
Из гистограммы видно, что большинство измерений имеют ошибку меньше 0.15·10-2-0.2·10-2. То есть, даже при самом удачном раскладе точность предсказания не будет выше этих 0.15 %-0.2 %.
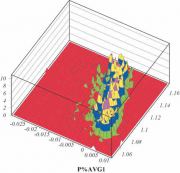
После того, как мы убрали основную (временную) зависимость, можно проверить, зависит ли изучаемая переменная от давления (P) и магнитного поля (H). Для этого воспользуемся способностью PAW создавать и отображать двумерные гистограмм:
#создаем двумерную гистограмму: давление от avg1 PAW > ve/pl P%avg1 10 #изобразим двумерную гистограмму 10 в виде поверхности PAW > SURF 10 65 -30 1
Обратите внимание на разделитель % между векторами в команде VECTOR/PLOT. Значениям первого вектора противопоставляется ось ординат (ось Y), а значениям второго ось абсцисс (ось X).
Команда HISTOGRAMgfv/2D_PLOT/SURFACE [ID THETA PHI CHOPT] (help surf) позволяет отобразить двумерную гистограмму в виде поверхности. Здесь ID — номер гистограммы, THETA и PHI — углы поворота гистограммы и в сферической системе координат, CHOPT - опции изображения.
Из картинки справа видно, что какая-то зависимость есть — избавимся от нее, как это было сделано с временной зависимостью. В результате подгонки сначала для давления, а потом для поля можно получить еще две формулы:
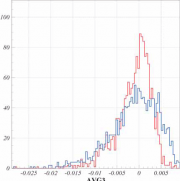
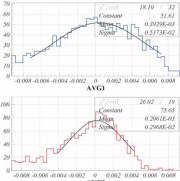
#поправка на давление PAW > sigma avg2=avg1-0.10901+0.99336E-01*P #поправка на магнитное поле PAW > sigma avg3=avg2+0.10844E-01-0.18258E-02*H #сравниваем две гистограммы до и после поправок #на давление и магнитное поле #переключаем цвет на красный PAW > set hcol 2 #рисуем гистограмму по значениям вектора PAW > ve/plot avg3 #переключаем цвет на синий PAW > set hcol 4 #рисуем вторую гистограмму поверх ‘s’ - superimpose PAW > ve/plot avg1 ! ‘s’
Обратите внимание на команду SET (help GRAPHICS/SET). Эта инструкция позволяет менять параметры графического представления данных. Если запустить ее без опций, то будет выдан список переменных, которые устанавливаются с помощью этой команды.
На рисунке справа представлены две гистограммы. Красная — конечный результат, а синяя — то, что осталось после исключения временной зависимости. Очевидно, что после учета давления и поля разброс уменьшился. Несимметричность гистограмм указывает на то, что временная зависимость на самом деле нелинейная. В реальности при подгонке использовалась экспоненциальная зависимость плюс некоторая константа. Выбор подгоночной функции был продиктован физической моделью явления, но по большому счету на этом временном интервале она не сильно отличается от обычной прямой.
В результате всех действий была получена зависимость:
AVG=3.46+2.29•10-9-9*time-9.9*10-2-2P+1.8*10-3-3H
Эта функция позволяет предсказывать исследуемое значение в зависимости от времени, давления и магнитного поля, но какова точность этого предсказания? Для ее оценки достаточно получить распределение разницы значений между экспериментальными точками и данной зависимостью, а затем взять его ширину. Можно просто оценить ширину распределения «на глазок», посмотрев на обсуждаемый рисунок, а можно получить ее из известной функции, более-менее описывающей это распределение, например, из функции Гаусса:
#создаем из значений вектора avg1 гистограмму N11 PAW > ve/plot avg1 11 #подгоняем гистограмму N11 в диапазоне (-0.007,0.007) #функцией Гаусса (G - Gauss) PAW > hi/fit 11(-0.007:0.007) G … EXT PARAMETER … NO. NAME VALUE ERROR … 1 Constant 51.608 1.9494 … 2 Mean 0.39292E-03 0.20076E-03 … 3 Sigma 0.51728E-02 0.27301E-03 … … #создаем из значений вектора avg3 гистограмму N13 PAW > ve/plot avg3 13 PAW > hi/fit 13(-0.004:0.004) G … EXT PARAMETER … NO. NAME VALUE ERROR … 1 Constant 75.655 3.0477 … 2 Mean 0.20614E-03 0.11857E-03 … 3 Sigma 0.29684E-02 0.16655E-03 … … #делим графическое окно на две зоны по оси ординат (help zone) PAW > zone 1 2 #меняем цвет гистограммы на синий PAW > set hcol 4 #рисуем гистограмму в диапазоне (-0.009,0.009) PAW > hi/pl 11(-0.009:0.009) #меняем цвет гистограммы на красный PAW > set hcol 2 PAW > hi/pl 13(-0.009:0.009)
Из всех значений в данном случае интересно только значение ширины распределения, или SIGMA[1].
Если учитывать только временную зависимость, то точность предсказания будет примерно 0.52 %, если же учесть давление и магнитное поле, то точность улучшится до 0.30 %, что существенно хуже идеальных 0.15-0.2 %. Очевидно, что остались еще какие-то неучтенные систематики.
Оценим, какую систематику удалось выбрать, учтя зависимость от давления и магнитного поля. Для этого воспользуемся системой COMIS (help comis):
PAW > comis PAW CS> type sqrt(0.52**2-0.30**2) MND> end *T SQRT(0.52**2-0.30**2) = 0.4247352 PAW CS> end
В общем, неплохо. Кстати, более тщательный анализ никаких кардинальных улучшений не дал — удалось только уменьшить «хвосты» и сделать итоговое распределение более симметричным за счет выбора более сложной подгоночной функции.
Быстрый анализ позволяет оценить, к какой точности имеет смысл стремиться. Это очень важно, так как сложность получения большей точности увеличивается от требуемой точности существенно нелинейным образом. Фактически на только что изложенный анализ по разным причинам ушел примерно месяц реального времени. Правда, основные проблемы были вовсе не технические. В частности очень много времени ушло на осознание, что исследуемая величина зависит от времени — это не казалось очевидным.
Ntuple
То, что только что было сделано с помощью векторов можно проделать с помощью ntuple. Для этого надо сначала создать ntuple (NTUPLE/CREATE), а затем считать в него текстовый файл (NTUPLE/READ).
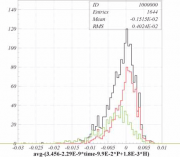
# создаем ntuple c ID=1 PAW > nt/cre 1 ‘LKr quality’ 6 ! ! time run avg er P H #читаем в ntuple с ID 1 текстовый файл PAW > nt/read 1 lkravg.dat ==> 1644 events have been read PAW > nt/print 1 ***************************************************************** * NTUPLE ID= 1 ENTRIES= 1644 LKr quality ***************************************************************** * Var numb * Name * Lower * Upper * ***************************************************************** * 1 * TIME * 0.109828E+10 * 0.113892E+10 * * 2 * RUN * 0.406400E+04 * 0.709400E+04 * * 3 * AVG * 0.742800E+00 * 0.846400E+00 * * 4 * ER * 0.700000E-03 * 0.201000E-01 * * 5 * P * 0.104400E+01 * 0.116000E+01 * * 6 * H * 0.000000E+00 * 0.704971E+01 * ***************************************************************** #включаем отображение статистики PAW > opt stat #отрисовываем разницу между экспериментом и предсказанием #с различным ограничением на величину ошибки er PAW > set hcol 1 PAW > nt/pl 1.avg-(3.456-2.29E-9*time-9.9E-2*P+1.8E-3*H) PAW > set hcol 2 PAW > nt/pl 1.avg-(3.456-2.29E-9*time-9.9E-2*P+1.8E-3*H) er<0.0015 ! ! ! ‘s’ PAW > set hcol 3 PAW > nt/pl 1.avg-(3.456-2.29E-9*time-9.9E-2*P+1.8E-3*H) er>0.0015 ! ! ! ‘s’
Преимущество при использовании ntuple заключается в том, что интерактивно можно накладывать условия для фильтрации данных. Как правило, ntuple создаются с помощью внешних программ, а PAW используется уже для интерактивного анализа. В стандартной документации к PAW очень подробно описано, как это делается.
Гистограммы
Гистограммы — это базовые объекты PAW. Непосредственно перед отображением данные почти всегда преобразуются в одно- или двумерную гистограмму. На гистограмму можно просто смотреть, а можно подгонять какой-либо теоретической зависимостью (HISTOGRAM/FIT).
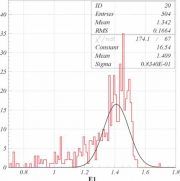
#поиск rz-файлов в базовой директории (файл создан внешней программой) PAW > sh ls *.rz ee-ang.rz #чтение файла #известно что в файле есть ntuple c ID=1 PAW > hi/fil 1 ee-ang.rz #создаем гистограмм N20 из переменной E1 с некоторыми условиями PAW > nt/plot 1.E1 f1=11&&f2=-11&&E1<2 ! ! ! ! 20 #подгоняем гистограмму распределением Гаусса PAW > hi/fit 20 G
Из рисунка видно, что наблюдаемое распределение функцией Гаусса не подгоняется. Надо что-то делать. Очевидно, что теоретическая функция должна быть как минимум несимметрична. Для этой цели подойдет так называемый логарифмический гаусс. Для подгонки надо создать файл loggaus.for примерно следующего содержания:
C Файл loggaus.for real function loggaus(x) C С помощью этого common-блока PAW получает доступ C к параметрам функции common/PAWPAR/PAR(4) sqrtln4=1.177410022515475 A=PAR(1) pike=PAR(2) sigma=PAR(3)*pike/100. assim=PAR(4) loggaus=0. if (abs(assim).le.1.E-6) then assim=sign(1.E-6,assim) endif if (sigma.le.0.) goto 10 xx=1.+sinh(assim*sqrtln4)/sqrtln4*(x-pike)/sigma if (xx<1.E-07) goto 10 loggaus=A*exp(-((log(xx)/assim)**2+assim**2)/2.) 10 continue end
Функция зависит от четырех параметров: A — амплитуда, pike - местоположение пика, sigma — ширины распределения в процентах, assim — асимметрии.
#создаем вектор параметров с начальными значениями PAW > ve/cre par(4) r 25. 1.4 5. 0. # создаем вектор с минимально допустимыми значениями (на глазок) PAW > ve/cre pmin(4) r 10. 1.3 1. -1. # создаем вектор с максимально допустимыми значениями PAW > ve/cre pmax(4) r 40. 1.5 10. 1. # создаем вектор, для ошибок подгонки PAW > ve/cre err(4) r # просим PAW подогнать распределение теоретической функцией # опции подгонки: # B - учитывать минимально/максимально допустимые значения # M - перейти интерактивную сессию Minuit # M обычно не используется, так как действия PAW при подгонке # по умолчанию вполне разумны PAW > hi/fit 20 loggaus.for “BM” 4 par ! pmin pmax err … # задаем имена параметров Minuit > name 1 A Minuit > name 2 pike Minuit > name 3 sigma Minuit > name 4 assim # задаем метод минимизации (migrad, обычно, самый подходящий) Minuit > migrad # просим попробовать улучшить подгонку (дольше, но чуть точнее) Minuit > improve … Minuit > exit … #смотрим результаты подгонки PAW > ve/print par PAR(1) = 35.4279 PAR(2) = 1.4809 PAR(3) = 4.30618 PAR(4) = -0.999999 #смотрим ошибки PAW > ve/print err ERR(1) = 3.61113 ERR(2) = 0.00484378 ERR(3) = 0.339507 ERR(4) = 0.174973 #нарисовать гистограмму 20 еще раз # e - рисовать статистические ошибки в бинах PAW > hi/plot 20 e
При подгонке этого распределения основной интерес представляло его ширина: =(4.3±0.3)%. Важно не только значение подгонки, но и оценка ошибки. Например, результат для sigma отличается от того, что должно быть в идеале больше чем на десять ошибок — можно сделать вывод, что есть какая-то, даже не проблема, а «плюха».
Функции
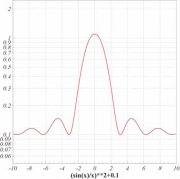
Функции также являются базовым объектом для PAW. Для отрисовки одномерных функций используется команда FUNCTION/PLOT.
#включить логарифмический масштаб для оси Y PAW > opt logy #нарисовать одномерную функцию PAW > fun/plot (sin(x)/x)**2+0.1 -10 10 #вернуться к линейному масштабу для оси Y PAW > opt liny
Обратите внимание на инструкцию opt (help GRAPHICS/OPTION). Эта инструкция по своим функциям схожа с командой set, но в отличии от нее отвечает за организацию представления данных, а не за графическое оформление.
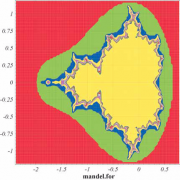
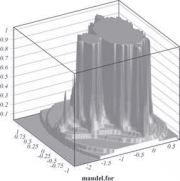
Работу с двумерными функциями продемонстрируем на классическом фрактальном изображении имени Мандельброта. Создадим код на FORTRAN:
C Из официальной документации к PAW C Файл mandel.for real function MANDEL(XP) dimension XP(2) data NMAX/30/ x=XP(1) y=XP(2) xx=0. yy=0. do n=1,NMAX tt=xx*xx-yy*yy+x yy=2.*xx*yy+y xx=tt if (4..lt.xx*xx+yy*yy) goto 1 enddo 1 MANDEL=FLOAT(n)/FLOAT(NMAX) end
В случае двумерных функций проблема отображения стоит гораздо острее, чем у одномерных. Двумерные функции для отображения преобразуются в гистограммы (help fun2)
# По результатам вычисления mandel.for создаем гистограмму 10 PAW > fun2 10 mandel.for 100 −2.4 .8 100 −1.2 1.2 ‘ ‘ # Выводим гистограмму 10 как контур PAW > hi/pl 10 cont3 # Выводим гистограмму 10 как поверхность PAW > hi/pl 10 surf4
Если разрешение не удовлетворяет, то можно создать гистограмму не 100×100, как в примере, а 1000×1000.
Заключение
Объять необъятное совершенно не реально, особенно при лимите на объем текста. Официальная документация содержит около 500 страниц, причем, один алфавитный указатель занимает 17 страниц. PAW - матерый программный продукт, которому уже двадцать лет. Этому пакету есть достойный приемник, правда, не лишенный недостатков, но об этом в следующий раз.
- ↑ В случае гауссоподобного распределения в диапазоне (<x>- ,<x>+) лежит примерно 68 % от всех событий. <x> — среднее значение или MEAN, соответствует SIGMA