LXF72:PHP

Материал из Linuxformat.

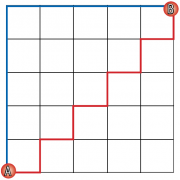
PHP A* ПоисК ПУти

Пол Хадсон (Paul Hudson) не может придумать, как выбраться из бумажного пакета, но он может написать программу поиска пути. если вы любитель создавать игры, можете за ним последовать. Исходный код — на прилагаемом диске.

Первая реализация игры Elite для BBC Micro занимала всего лишь 22 килобайта, но в ней вы могли до бесконечности летать от звезды к звезде и исследовать новые планеты. Конечно, большая часть этих звёзд была сгенерирована с помощью случайных чисел, и именно поэтому вы могли путешествовать очень долго без необходимости в тысячах дискет. В Elite выполнялось главное правило создания игр — не надо хранить то, что можно очень быстро сгенерировать. Для карт это значит, что нет смысла хранить все возможные маршруты ваших искусственных существ, вместо этого лучше использовать алгоритм поиска пути, благодаря которому они смогут перемещаться в изменяющемся окружении, демонстрируя некоторый интеллект.

всё, что есть на свете

Существует два популярных алгоритма поиска пути, и они распространены по разным причинам. Первый называется алгоритмом Дейкстры (он так же известен как алгоритм заливки), и он популярен так как его просто программировать. Второй называется A* (читается как «А-звёздочка»), и он популярен потому, что быстр. В этой статье мы рассмотрим алгоритм А*, широко используемый в игровой индустрии. Суть в том, что алгоритм Дейкстры на самом деле лучше, так как он всегда находит кратчайший путь от точки А в точку б, тогда как А* очень эффективен при поиске очень хороших маршрутов, но они не обязательно оказываются оптимальными.

Алгоритм заливки так называется потому, что он делает поиск в ширину — он ищет все возможные пути вокруг точки А перед тем, как увеличить радиус поиска. Если мы оценим в одну единицу перемещение из квадрата в любой из восьми соседних, то мы сможем оценивать сложность пути — перемещение на два квадрата будет стоить две единицы, перемещение на три — три и так далее. Выполняя «заливку», мы оцениваем длину пути для каждого квадратика на игровой доске, даже после того, как алгоритм добрался до целевой точки. Это необходимо, так как идеальный путь может требовать обойти целевую точку и затем вернуться к ней с противоположной стороны.

А* вместо этого использует эвристическую оценку предполагаемого расстояния между текущей точкой и целью маршрута. здесь нам придётся изменить терминологию — мы будем называть квадратики «узлами», так как алгоритм А* одинаково хорошо работает для квадратиков, шестиугольников и додекаэдров. Эвристикой будем называть функцию, которая помогает найти расстояние до следующего узла - оно может быть определено неправильно, но мы надеемся что оно окажется близко к истине. Эвристика, которой мы будем пользоваться, полагается на Манхэттенское расстояние между точками, иначе называемое «геометрия таксиста». Этот показатель называется так потому, что остров Манхэттен в нью йорке имеет прямоугольную планировку, и если вы начали путь в точке А и закончили в точке б, то не имеет значения, какой маршрут вы избрали, поскольку длина у них у всех одинаковая.

Для ясности давайте введём персонажа, который ищет дорогу, а вместо точек А и б будем говорить Старт и Финиш.

вслед за магией

Манхэттенское расстояние обозначает, что не важно, по какому маршруту вы доберётесь из точки А в точку B — пройденное расстояние получится одинаковым.

Алгоритм А* включает в себя три важных компонента — два массива узлов под названиями «открытый список» и «закрытый список» и наша эвристическая функция.

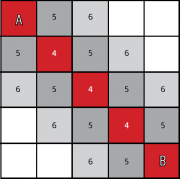
Узел Старта (или точка А) добавляется к открытому списку, значит, мы должны рассматривать её как часть пути. затем мы используем эвристику, чтобы оценить путь от старта до финиша. Поскольку мы используем манхэттенское расстояние, и поскольку первая версия нашего алгоритма оценивает движение по диагонали как эквивалентное движению вдоль стороны квадрата, эвристике достаточно вычесть координату X финиша из координаты X старта, затем так же вычесть координаты Y и взять максимальную из полученных разностей. однако это ещё не всё, мы знаем расстояние до финиша, но нам так же нужно и расстояние до старта, а так же их суммарное значение (которое будем называть суммарным расстоянием).

хранить расстояние до старта важно, так как оно поможет нашему персонажу найти самый короткий путь. При подсчёте эвристики для данного узла мы должны передать ей расстояние до старта от предыдущего узла маршрута (того, который добавил данный узел в открытый список), для того чтобы правильно подсчитать пройденный путь. После подсчёта эвристики для стартового узла мы входим в цикл. В цикле мы будем искать возможность добавить новый узел в открытый список до тех пор, пока он не опустеет или пока мы не найдём путь до финиша. Если мы пока не добрались до финиша и в открытом списке ещё есть элементы, возьмём из него элемент с минимальным суммарным расстоянием. В начале в открытом списке всего один элемент — старт — так что мы выберем именно его. затем мы должны добавить все узлы вокруг старта в открытый список, подсчитав для каждого из них эвристику. В финале переместим выбранный узел (Старт на первом шаге) из открытого списка в закрытый, так как мы знаем, что уже обработали его.

на втором шаге цикла в открытом списке уже больше элементов, так как там находятся все узлы, соседствующие со стартом. найдём среди них элемент с минимальным суммарным расстоянием — и добавим всех его соседей в открытый список (кроме тех, которые уже находятся в закрытом списке, так что Старт в открытый список повторно не попадёт).

цикл будет продолжаться до тех пор, пока открытый список не опустеет (что значит что нужного пути не существует) или пока Финиш не попадёт в закрытый список — что значит мы нашли путь к нему.

Правила

нет причин скрывать — этот код скорее всего будет самым сложным из всего, что вы писали раньше. Проблема в том, что алгоритм А* настолько сложен, что скорее всего потребует использования PHP-отладчика, иначе вы можете провести очень много времени, гуляя кругами и удивляясь, почему ваша программа падает, или почему персонаж забредает в никуда.

Это ещё ничего. однако, вдобавок ко всем нашим проблемам мы собираемся использовать ncurses, библиотеку для текстовой графики из LXF69. использование ncurses требует компиляции вашей собственной версии php, с включённой поддержкой этой библиотеки. А это значит, что вы не сможете воспользоваться нестандартным отладчиком, например входящим в Zend Studio, поскольку он может работать только с вполне конкретной версией PHP — именно с той, с которой отладчик был скомпилирован.

Кроме того, это значит что вы не сможете отлаживать программу при помощи большого числа операторов print в коде, так как их просто не будет видно, поскольку ncurses занимает весь экран целиком. и хотя вы увидите ошибку, из-за которой работа сценария прекращается, понять её без помощи KSnapshot будет довольно затруднительно.

итак, сочетание из А* и ncurses обозначает тяжёлую работу. но чтобы оправдать заработанные тяжким трудом деньги, которые вы заплатили за LXF, мы проделали эту работу сами! Так что вы обнаружите на прилагаемом к журналу диске код, готовый к использованию. Поэтому давайте просто посмотрим, как он работает.

Весь сценарий, кроме последней пары страницы кода состоит из функций — пропустим их пока. Внизу вы увидите обычный код ncurses для инициализации экрана и получения его размеров, но тут есть несколько важных моментов.

Глобальные переменные — а тут их несколько — записываются буквами в верхнем регистре. $LETTER_RANGE — это массив символов от A до Z; он сделан глобальным для того, чтобы не пересоздавать его каждый раз, когда он понадобится. $CURRENT_POS — это координаты точки, в которой находится персонаж. заметьте, что мы используем метод «через коридор вверх по лестнице», то есть номер колонки стоит перед номером строки. Колонки нумеруются от A до Z, а строки от 1 до максимально доступного числа.

Продолжаем. $prompt содержит текст, который мы покажем на экране как инструкцию для пользователя. Мы хотим, чтобы люди могли ввести тут координаты ячейки, так что у этой же области экрана должна быть возможность получить и интерпретировать ввод пользователя. Это делается при помощи глобальной переменной $LIVE_PROMPT, которая изначально принимает значение $prompt. Когда пользователь вводит текст, он добавляется к $LIVE_PROMPT, так что вы можете видеть то, что набираете. После нажатия на Enter переменная $prompt используется, чтобы вернуть $LIVE_PROMPT изначальное значение.

После вызова функции drawgrid(), которую я вскоре опишу, код входит в бесконечный цикл с помощью оператора while(1). Вызов ncurses_wgetch() выполняет ожидание, пока не будет нажата какая-либо клавиша, а по нажатию мы входим в оператор switch для выбора нужного действия. Если код нажатой клавиши равен 13 (то есть если это Enter), то мы обрабатываем ввод пользователя, иначе просто добавляем введённую букву к $LIVE_PROMPT и перерисовываем экран.

По нажатию Enter выполняется простейшая проверку ошибок. было ли введено точно два символа? является ли первый символ буквой? является ли второй цифрой? Если все эти условия были выполнены, вызывается функция makemove() для поиска пути от старта до финиша, $prompt сбрасывается и сетка рисуется заново.

итак, это мы рассмотрели основную часть кода. Выше вы найдёте функции resetgrid() для очистки данных, drawgrid() для рисования сетки, функция handlenode() принимает узел и рассматривает, которых из его соседей можно использовать. Функция calc_distance() рассчитывает эвристику, а makemove() настраивает открытый и закрытый списки и вызывает handlenode() до тех пор, пока путь не будет найден, а затем обновляет сетку, чтобы показать маршрут.

resetgrid()

Функция resetgrid() создаёт и заполняет двумерный массив $DATA, который содержит все ячейки сетки и их значения. Первое измерение массива — это номер строки, второе — номер столбца. В каждом элементе массива содержится строка, которая отображается в нужной ячейке. По умолчанию в каждом элементе "" (пустая строка). Когда путь найден, в ячейках избранного маршрута содержится буква „z“, а в финальной точке — буква „c“.

Массив настраивается циклом от нуля до $MAX_ROW делённого на два, это сделано потому, что в сетке нужно пространство для отображения содержимого. Вложенный цикл добавляет массиву второе измерение и одновременно заполняет его пустыми значениями.

calc_distance()

А* так быстр потому, что он проверяет только близкие к маршруту узлы. Серым цветом помечены проверенные узлы, а красным — избранные узлы маршрута. Число в центре обозначает суммарное расстояние — сумму пути до этого узла от старта (точка А) и от узла до финиша (точка B).

calc_distance() — это наш эвристический калькулятор. Он вызывается каждый раз, когда надо оценить длину пути от одного узла до другого. О на состоит всего из четырёх строчек, но это самые важные строчки в программе, поскольку именно они определяют, которая из ячеек будет выбрана как следующая на пути к финишу. Первые две строки очень просты, это наша реализация подсчёта манхэттенского алгоритма. Помните, в сетке одинаково быстро можно как пройти сначала вверх на три блока, а потом вправо на три блока, так и вверх-вправо-вверх-вправо-вверх-вправо. Б олее того, поскольку мы трактуем диагональный переход равным переходу вдоль стенки квадрата, манхэттенское расстояние от старта до финиша всегда будет максимальным из расстояний вдоль оси X или Y. Н апример, если финиш четырьмя узлами правее старта и двумя узлами выше, то потребуется пройти четыре узла, чтобы попасть куда нужно.

Вернёмся к коду. Первая строка получает номер колонки из его ASCII-эквивалента при помощи функции ord(). Н апример, 65 — это ASCII-код латинской буквы A. Когда мы вычитаем два полученных числа друг из друга, то получаем расстояние между двумя колонками. Если финиш левее, чем старт, то это даст нам отрицательное число, поэтому воспользуемся функцией abs(), чтобы сделать его положительным. В третьей строке при помощи функции max() мы получим большее число из двух, позволяющее нам эвристически оценить расстояние от старта до финиша.

Важно заметить, что эвристическая оценка чаще всего оказывается заниженной. В простейшем примере, который мы имеем, манхэттенское расстояние — это действительно минимальное расстояние от старта до финиша, то есть если манхэттенское расстояние равно четырём узлам, то персонажу придётся пройти именно четыре узла.

Это не всегда оказывается верным. Если на пути есть препятствия, или если у вас есть различные типы поверхности, которые могут замедлять путь персонажа, то манхеттенское расстояние окажется заниженным. Поэтому правильным будет сообщать расстояние от старта до финиша для „птичьего полёта“, тогда как реальный путь окажется значительно медленнее. О днако, если наша эвристика завысит путь от старта до финиша, то полученный путь окажется неоптимальным, так что этот алгоритм попадёт в число неприемлемых (неспособных найти оптимальный путь).

Последняя строчка calc_distance() просто определяет возвращаемое значение, которое является массивом значений, содержащим суммарное расстояние (насколько хорош путь через этот узел), расстояние до старта и эвристику (как далеко мы от финиша по геометрии таксиста).

makemove()

Функция makemove() вызывается, когда пользователь ввёл правильные координаты и нажал ввод. Как уже упоминалось, алгоритму А* требуются открытый и закрытый списки узлов, в которых нужно искать и в которых поиск будет производиться в определённом порядке. В данной функции и создаются эти списки. В обоих массивах координаты узла используются в качестве ключа, а возвращённые из calc_distance() данные как значения (это массив, как говорилось чуть раньше).

Вся работа происходит в цикле while. В условиях цикла проверяется, что финиш не входит в закрытый список и что открытый список не пуст. Если это верно, то вызывается функция handlenode() и ей передаются открытый и закрытый списки. Когда цикл закончен, то есть мы нашли финиш, мы вносим в соответствующую ячейку символ „с“ и перерисовываем экран. З атем мы вызываем sleep(), из-за чего ничего не происходит целую секунду. Это нужно исключительно для красоты, чтобы вы успели полюбоваться изменениями на экране.

В конце концов, мы пробегаем по закрытому списку и задаём каждому его элементу значение „z“, отмечая, каким образом персонаж добрался до нужного места. И в конце концов обновляется значение переменной $CURRENT_POS, чтобы запомнить новое положение персонажа.

handlenode()

Функция handlenode() самая длинная, но вовсе не самая сложная. Больше всего места занимает поиск соседей нужной ячейки, которые нуждаются в проверке. Если диагональное перемещение стоит больше, чем перемещение вдоль стороны квадрата, то мы легко можем переработать этот код при помощи простого цикла — пройти строки от row-1 до row+1 и столбцы от col-1 до col+1, пропустив текущий узел. но по причине эквивалентности диагонали и простого смещения использование такого кода будет поощрять диагональные перемещения — вместо движения по прямой, персонаж начнёт чертить зигзаги на местности.

В первой части handlenode() происходит поиск лучшего узла для обработки. Это делается при помощи записи в $shortest_distance большого числа, и записи в $best_node нуля. затем происходит цикл по всем элементам открытого списка, сравнение каждого значения с $shortest_distance до тех пор, пока не обнаружится узел с самым коротким суммарным расстоянием. затем этот узел удаляется из открытого списка, происходит поиск соседей и они добавляются в открытый список. Узлы группируются в „колонку слева“, „текущую колонку“ и „колонку справа“, но нам достаточно обсудить только первую группу, чтобы понять их все.

итак, чтобы найти узлы в колонке слева от текущего узла, для начала нам надо проверить, что мы не находимся в колонке А, поскольку она уже является самой левой. Как мы видели в calc_distance(), функция ord() превращает букву в её ASCII-код. Если мы вычтем 1 из этого кода и преобразуем его обратно в символ, то B превратится в A, T в S и так далее. Поскольку теперь мы знаем имя колонки слева, нам надо проверить, входят ли верхний, средний и нижний квадратики из этой колонки в закрытый список, и если не входят - внести их в открытый список.

Как и в makemove(), тут мы используем координаты ячейки как ключ, а массив, полученный из calc_distance() — как значение. обратите внимание: в качестве первого параметра calc_distance() выступает путь до старта от текущего узла (то есть число перемещений, которое потребовалось, чтобы сюда попасть) плюс 1, так как до нового узла надо сделать ещё один шаг.

drawgrid()

Функция, которая делает рисование нашей таблички в ncurses ужасным по двум причинам. Во-первых, она использует ncurses, что само по себе превращает процесс отладки в ад. Во-вторых, в ней используются на первый взгляд произвольные числа для добавления или вычитания здесь и там, а я это ненавижу. что ж, это мой шанс записать их все на бумаге, чтобы никогда больше не забывать.

После использования ncurses_werase() для очистки экрана, переменная $gridrows устанавливается равной $MAX_ROW-4, что-бы оставить внизу место для подсказки пользователю. затем мы видим два цикла for, которые рисуют сетку. Первый из них рисует строки, начиная с 0 и до $gridrows, добавляя 2 каждый раз, чтобы оставить место для данных между линиями сетки. Каждая итерация цикла использует ncurses_wmove() для перемещения курсора к нужной строке, а затем ncurses_whline() для рисования горизонтальной линии. она принимает в качестве параметров экран для рисования, символ, которым будет рисовать, и длину линии. Функция ord() снова используется для того, чтобы превратить символ в его числовой эквивалент для функции.

Если $i больше 2, то есть если это третья или последующая строка цикла — наступило время выводить данные. Это не настолько случайно, как кажется: первая итерация цикла нарисовала внешнюю линию сетки, а вторая — заголовок (тот, в котором находится координатные обозначения), только в третьей строчке мы можем приступить к отображению данных. итак, вызовем ncurses_mvwaddstr() для вывода номера строки в самом левом столбике, а затем сбросим указатель массива $LETTER_RANGE, чтобы мы могли использовать его для выборки элементов из массива $DATA. Вот что делает внутренний цикл for — он перебирает элементы от 8 до $MAX_COL по 4 за раз. По сути, это то же самое, что мы делали со строками — мы начинаем с конца второго столбика, чтобы не писать поверх номеров строк.

Вызов ncurses_mvwaddstr() кажется очень сложным, но он разбивается на очень простые кусочки: нарисовать в нашей строке и колонке, используя половину $i как ключ массива $DATA и текущее значение $LETTER_RANGE как ключ ко второму измерению массива. Помните, $i увеличивается дважды на каждую строку данных, поэтому нам приходится делить её на два. Функция next() перемещает указатель текущего элемента в массиве $LETTER_RANGE на один элемент вперёд при каждом вызове, так что в результате мы печатаем $DATA[1]["a"], $DATA[1]["b"] и так далее.

После вывода всех строк reset() возвращает указатель $LETTER_RANGE обратно к «A», так что мы можем отобразить вертикальные линии. В этот раз счётчик пробегает от 0 до $MAX_COL, так что мы можем заодно нарисовать края сетки и линию справа от номеров строк. Поскольку в этот раз мы рисуем столбики, функция ncurses_wvline() вызывается, чтобы напечатать символ "|" сверху вниз. Как и со строками, если значение больше 4 (мы используем 4 вместо 2, чтобы сделать сетку квадратной), то надо заодно отобразить заголовки столбцов.

В конце концов мы выводим подсказку внизу экрана и вызываем ncurses_wrefresh(), чтобы обновить это всё.

ну теперь всё?

я думаю, вы согласитесь, что одолеть всё это было довольно сложно. использование ncurses уже непросто, а с применением сложных алгоритмов программа делается совсем мудрёной. но теперь тяжёлая работа закончена, вы может запустить программу и получать удовольствие: у вас есть полноценная реализация алгоритма А* на php, а я думаю что это ужасно круто. Конечно, она не совершенна — посмотрите на врезку «Домашнее задание», и у вас найдётся занятие на весь месяц ожидания следую-