- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF139:School1
Материал из Linuxformat.
- Школа LXF Обмен опытом и передовые идеи по использованию свободного ПО в образовании
Содержание |
Linux на уроках физики
- Вооружившись дистрибутивом EduMandriva 2010 Spring LXDE DVD, Анна Трефилова покажет, как на радость школьникам учинить на уроках пальбу, не причинив ущерба.
С овременные школьники с энтузиазмом воспринимают внедрение новых информационных технологий в учебный процесс. Рассмотрим, как отобрать наиболее удобное и интересное с методической точки зрения ПО, с максимальной пользой применимое для преподавания физики в школе.
Уровень усвоения школьником учебного материала по физике можно определить путем оценки степени понимания им физической сущности изучаемого явления. Важную роль в процессе понимания играет учебный физический эксперимент, позволяющий пронаблюдать результаты воздействия на систему при определенных начальных условиях. Полученные результаты анализируются, и делаются выводы о физической сущности явления. При всей своей важности и наглядности, а также достоверности и доказательности, натурный эксперимент не всегда открывает полную картину происходящего процесса. Действительно, в большинстве случаев наблюдатель видит начальное и конечное состояние системы; промежуточные же состояния часто оказываются недоступными для наблюдения. В то же время, именно процесс в динамике наиболее полно отражает физическую сущность наблюдаемого явления. Ученые для глубокого изучения явления прибегают к его моделированию. Разработаны принципы создания модели, наиболее полно отражающей существенные свойства изучаемого объекта или явления.
Рис. 1. Изначально перед нами чистое поле для нашей деятельности.
При изучении физики в школе моделирование применяется широко: например, исследуются модели материальной точки, идеального газа, математического маятника и др. Этих объектов нет в природе, но реальные объекты при определенных условиях приближаются по своим свойствам к этим моделям. Иными словами, построение физической теории, описывающей идеальные объекты (то есть модели), позволяет изучить закономерности реальных процессов и явлений природы, а затем применить полученные знания для улучшения жизни и деятельности человека. Компьютерное моделирование, помимо прочих своих достоинств, позво-ляет визуализировать идеальные модели и наблюдать за физическими процессами в динамике; фиксация промежуточных результатов дает возможность сделать выводы о закономерностях, а следовательно, и о физической сущности явления.
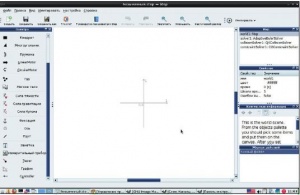
Для моделирования учебных физических экспериментов предлагаем воспользоваться пакетом KDE4 Step. При запуске Step откроется окно так называемого мира, в котором поначалу ничего нет, кроме системы координат, расположенной в центре (рис. 1).
Система координат позволяет с большой точностью строить модель физического опыта. Слева от мира находится палитра элементов, которые можно в нем разместить. Справа четыре панели: список элементов мира, список свойств выбранного элемента, контекстная информация для выбранного элемента и журнал действий. При первом знакомстве с программой рекомендуем просмотреть учебные примеры руководства: они дают представление об основных возможностях Step. Это можно сделать, выбрав в меню «Файл > Открыть Примеры» нужный пример. Далее нажимаем кнопку «Имитировать» и наблюдаем, что происходит. По окончании нажимаем кнопку «Остановить».
Простые физические опыты
Рис. 2. Знакомый со школы пример — тело покоится на плоскости.
Интерфейс программы интуитивно понятен, а возможности очень велики. Например, разработав серию простых заданий по динамике, можно успешно закреплять понятие силы, в том числе осознанность построения векторов сил на физических рисунках.
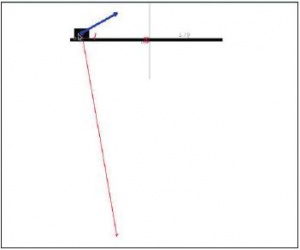
На рис. 2 показан пример, когда к телу, находящемуся на горизонтальной плоскости, приложена сила, направленная под углом к горизонту. Рисуем прямоугольник с помощью элемента Квадрат, размещаем его на горизонтальной плоскости (тоже квадрат), закрепляем плоскость с помощью фиксации и прикладываем к центру тела силу LinearMotor. Величину силы задаем справа в панели «Свойства». Чтобы направить силу под углом к горизонту, захватываем мышью конец вектора и поворачиваем, как нужно. Теперь добавим силу тяжести, выбрав ее в палитре элементов и щелкнув мышью в любом месте мира. Сила эта не отображается, но если навести курсор на тело, то появится результирующая двух сил – силы тяжести и приложенной силы. Учащиеся могут отразить в отчете построение этой результирующей силы, опираясь на результаты работы программы. Нажав кнопку «Имитировать», пронаблюдаем, как тело движется сначала медленно, а затем все быстрее, то есть результирующая придает телу ускорение. В любой момент можно остановить движение кнопкой Остановить и отметить все свойства тела в этой точке траектории.
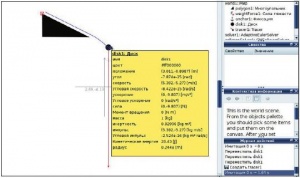
На рис. 3 показан пример тела, скользящего по наклонной плоскости. Наклонная плоскость построена с помощью элемента Многоугольник, закрепленного фиксацией. Траектория визуализирована с помощью элемента Tracer, расположенного на диске. Кроме силы тяжести, на диск никакие силы не действуют. Имитация остановлена в точке, когда тело свободно падает с некоторой начальной скоростью. При наведении курсора на тело получаем список его свойств, позволяющий отслеживать промежуточные результаты, что невозможно в натурном эксперименте.
Рис. 3. Тело на наклонной плоскости не может не покатиться.
Рассмотрим еще один пример – модель нелинейных колебаний. Создадим в мире объект Прямоугольник, который будет являться неподвижным; на нем в дальнейшем расположим точку подвеса сложного маятника. Зададим координаты для объекта box1: справа в разделе «Свойства» в поле «Положение» введем значение (0,2.5)[m]. Зафиксируем объект с помощью элемента «Фиксация». Создадим тело маятника – диск и расположим его в точке с координатами (0,0.5). Соединим disk1 и box1 элементом Прут, задав для него локальные координаты, то есть координаты относительно тела, к которому прут прикреплен:
localPosition1=0,0 и localPosition2=0,0.
Подобным образом построим второе тело, соединив его прутом с первым телом. Для визуализации траектории колебаний маятника расположим элементы Tracer на обоих дисках, также определив локальные координаты как (0,0). Наконец, зададим наличие силы тяжести.
Рис. 4. Исходный маятник пребывает в состоянии покоя.
Рис. 5. Приводим систему в нужное для моделирования состояние.
Рис. 6. Колебания сложного маятника без физически сложного маятника.
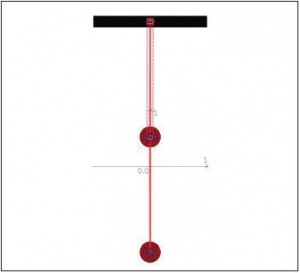
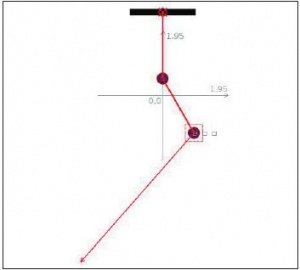
Теперь отклоним маятник на рис. 4 от положения равновесия, взяв мышью за нижнее тело (рис. 5). Программа при этом покажет результирующую действующих на тело сил: силы тяжести и силы натяжения нити. При отклонении маятника следите за тем, чтобы не сместить точку крепления прута с верхним телом.
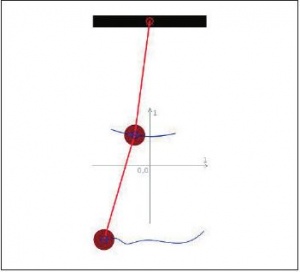
Нажимаем кнопку «Имитировать» и наблюдаем колебания сложного маятника (рис. 6). В натурном физическом эксперименте весьма сложно визуализировать траектории каждого из тел такого маятника. Так как нелинейные колебания рассматриваются в школе без математического описания, то достаточно продемонстрировать учащимся (а лучше самим создать) такой виртуальный эксперимент после наблюдения натурного. Тогда школьники могут оценить достоверность компьютерной модели на уровне человеческого восприятия, без математических расчетов, и увидеть траекторию движения каждого из тел маятника.
Мы описали лишь простейшие задания, иллюстрирующие большой методический потенциал программы Step для преподавания физики в школе. В действительности можно создавать очень сложные модели реальных объектов и явлений, исследовать их работу, подтверждая физическую теорию, которая описывает идеальные физические модели. Как видно из экранных снимков, инструментарий Step довольно обширен. Можно охватить кинематику, динамику, электростатику, закон всемирного тяготения, газовые законы. Особенно интересно школьникам создавать действующие механизмы и наблюдать их работу.
Физическая «песочница»
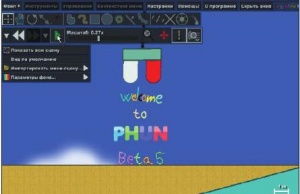
Для учащихся более привлекательным оказался Phun (рис. 7), иначе называемый «2D-песочницей для физиков». Программа англоязычная, но после пятой версии возможна русификация, выбором опции Russian в меню File в пункте Change language. Среда позволяет создавать модели объектов и явлений с учетом физических параметров, предлагая ряд инструментов и функций. При наведении курсора мыши на инструмент высвечивается его название и краткая инструкция по применению. Веселая начальная сцена сразу же покажет Phun в действии: намагниченные буковки притягиваются к магниту, остальные падают, затем выкатывается диск с надписью killer и проглатывает упавшие буковки…
Рис. 7. Phun изначально выглядит достаточно необычно.
Уже из этой сцены видны богатые возможности программы. Для начала работы над моделью нужно создать новую сцену: «Файл > Новая сцена». Каждому объекту можно задать свойства, выбрав его на сцене. Если нажата кнопка Контекстное меню в основном меню программы, то под основным меню появляется контекстное меню, содержащее список возможных настроек для данного объекта. Контекстное меню всегда можно убрать с помощью той же кнопки основного меню. Создав модель, нажимаем кнопку пуска (зеленый треугольник) и запускаем процесс. Если результат не удовлетворяет, отменяем последние изменения кнопкой отката (как в интерфейсе музыкального плейера). Помимо основных инструментов создания объектов, есть еще две кнопки: кнопка наличия силы тяжести и кнопка наличия сопротивления среды. Выбираем их в зависимости от задач моделируемого эксперимента.
На основе простейшего опыта покажем, как построить его модель. Из пружинного пистолета стреляют в горизонтальном направлении. Задание: определить, как зависит дальность полета снаряда от жесткости пружины пистолета. Реально такой эксперимент очень сложно провести, но он интересен для формирования понятия энергии, изучения закона сохранения энергии.
Строим бесконечную плоскость поверхности земли. На некоторой высоте размещаем пистолет с помощью инструмента Полигон в виде жирной буквы П, лежащей на боку. Фиксируем пистолет в двух точках. Можно построить пистолет и из прямоугольников, тогда их нужно будет скреплять между собой. Расположим внутри пистолета шарик и соединим его пружиной с дном пистолета. Пружина всегда соединяет два объекта; ее жесткость можно задать в контекстном меню свойств.
Рис. 8. Выстрел из пистолета — с Phun это возможно без жертв и разрушений.
Рис. 9. Меняем калибр нашего огнестрельного орудия.
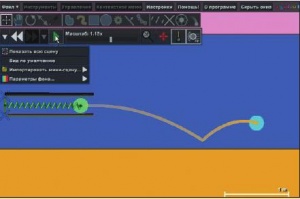
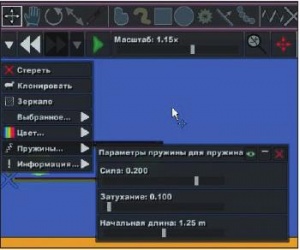
Передвигаем шарик, сжимая пружину. Рисуем второй шарик на месте первого – это снаряд. На снаряде располагаем след, уменьшив его, если нужно. Проверяем, нажата ли кнопка наличия силы тяжести. Запускаем (рис. 8) и наблюдаем, как вылетает снаряд, как отскакивает от поверхности земли. Используя расположенный внизу масштаб, оцениваем дальность полета снаряда. Отменяем результаты имитации и изменяем жесткость пружины (рис. 9): выделяем пружину левой кнопкой мыши, в контекстном меню выбираем пункт Пружины. В появившемся меню «Параметры пружины» для Пружина (это имя объекта) увеличим значение Силы (так обозначена здесь жесткость пружины). Вновь оценим дальность полета снаряда. Вывод: чем жестче пружина, тем дальше летит снаряд. Снаряд летит дальше при условии, что его начальная скорость больше. Увеличение скорости напрямую связано с увеличением кинетической энергии снаряда в момент выстрела. Энергия сжатой пружины характеризуется как ее потенциальная энергия, прямо зависящая от жесткости пружины. Потенциальная энергия сжатой пружины в момент выстрела превращается в кинетическую энергию снаряда по закону сохранения энергии, то есть скорость вылета снаряда тем больше, чем больше жесткость пружины.
Конечно же, в этом примере показана лишь малая часть возможностей Phun. В Интернете можно найти множество созданных в Phun моделей различных объектов, от простых до очень сложных. Также можно найти видеофильмы, демонстрирующие возможности Phun. Учитель может заранее заготовить модели для изучения на уроке, но можно также дать детям задание для самостоятельного моделирования изучаемого явления, вплоть до проведения конкурсов на самую интересную или самую сложную модель. Такие конкурсы повысят мотивацию детей к изучению физики. Кроме того, набравшись опыта, учитель может использовать Phun при объяснении нового материала, строя физические рисунки не мелом на доске, а с помощью компьютера и проектора.
Не только модели
Для проведения расчетов при решении задач или оформлении лабораторных работ можно воспользоваться программой SmathStudio (рис. 10). Интерфейс программы прост и интуитивно понятен; процесс введения формул, математических выражений и данных также не представляет сложности даже для новичка. На наш взгляд, использовать для осуществления расчетов программу более продуктивно, чем калькулятор. Внешний вид документа, отражающего расчет задачи, максимально приближен к естественному тетрадному варианту. Оформленные таким образом задания выглядят эстетично и позволяют формировать у учащихся умения, связанные не только с выполнением расчетов, но и с качественным оформлением документов. Программа умеет решать системы уравнений, как это показано в примере на рисунке, находить производные, интегралы, логарифмы. Самое, пожалуй, ценное – построение графиков простым способом. Чтобы построить график функции, выбираем в панели «Функции» опцию «2D» или «3D» и в появившемся окне внизу пишем название функции, для которой нужно построить график. Все графики строятся в координатных осях xOy. Также есть возможность вставки текстов, изменения цвета текста, фона. Можно вставлять единицы измерения и решать задачу с их учетом. В приведенном примере все величины измерены в СИ.
Рис. 10. Многим это напомнит проприетарный MathCad.
Рассмотрим задачу о построении траектории движения тела, брошенного под углом к горизонту с некоторой начальной скоростью. Эта задача вызывает известные трудности у девятиклассников, так как здесь уравнение движения представлено совокупностью проекций на оси Ox и Oy. При исследовании физической сущности задачи оказывается, что вдоль горизонтальной оси движение остается всегда равномерным, так как проекция ускорения свободного падения на эту ось равна нулю, а вдоль вертикальной оси движение сначала равнозамедленное, а затем равноускоренное. Вершина параболы, описывающей траекторию движения, есть точка, в которой проекция скорости на ось Oy равна нулю. Все эти моменты физической теории задачи необходимо учитывать при ее решении.
Коротко опишем процесс ввода задания для вычисления программой. В нашем случае задача сводится к нахождению зависимости y(x) при определенных начальных условиях. Зависимость должна быть выведена из системы уравнений x(t) и y(t). Условие задачи вводится с помощью инструмента «Текстовое поле», который находится в меню «Вставка». Рекомендуется с самых первых заданий приучать школьников к полному оформлению заданий, включая написание условия задачи, пояснений к данным и пояснений к действиям. Такое оформление задач, решенных с помощью математического пакета, имеет ту же методическую ценность, что и правильно оформленный тетрадный вариант.
Несомненным преимуществом является то, что дети учатся грамотно и понятно для вычислительной программы вводить данные для расчетов. Подобное умение в наш век компьютерных технологий пригодится в будущей профессиональной жизни практически любому специалисту. Далее мы рассмотрим один нюанс, который также можно применить в процессе обучения.
До ввода самой системы уравнений необходимо определить начальные условия задачи. Перечисляем их путем означивания констант: g = 9.8, x0 = 0 (то есть начало движения совпадает с началом отсчета по оси Ox) и т. д. Относительно угла между начальной скоростью тела и положительным направлением оси Ox необходимо помнить, что программа считает функции синуса и косинуса от радианной меры угла, поэтому, в конечном итоге значение угла должно быть выражено в радианах. Сделать это можно разными способами. Один из них заключается в использовании единиц измерения, другой в непосредственном пересчете значения из градусной меры угла в радианную. Мы выбрали второй вариант с тем, чтобы учащиеся, во-первых, запомнили (или вывели) формулу для нахождения радианной меры угла, зная его градусную меру, во-вторых, увидели преимущества использования математического пакета: нужно задать только формулу для вычисления, остальное программа делает сама.
Рис. 11. Увеличиваем число уравнений системы.
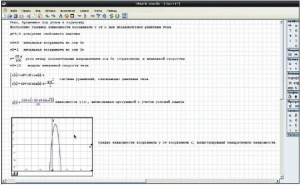
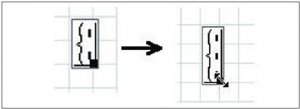
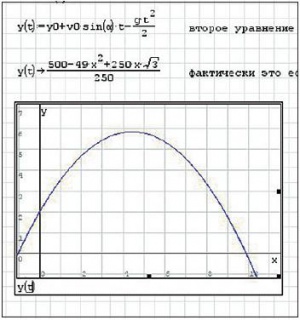
После того, как данные введены, оформляем систему уравнений, для чего справа в разделе «Функции» выбираем значок системы (фигурная скобка). В черных прямоугольниках вводим уравнения системы, не забывая определить зависимость x(t) и y(t). Если нужно ввести более двух уравнений, то, встав на нижний черный прямоугольник, нажимаем кнопку перемещения вправо на клавиатуре компьютера до тех пор, пока не появится уголок с черным квадратиком (рис. 11). Потянув за него вниз, определяем количество уравнений в системе. Далее вводим искомое уравнение, зависимость y(x), выбираем справа в разделе Арифметика знак и получаем нужное нам уравнение. Как-то проанализировать полученное уравнение очень сложно, так как оно получено с учетом начальных условий задачи и представлено в максимально упрощенном варианте (приведено к общему знаменателю).
График функции, построенный для этого уравнения, должен доказать его правильность. Парабола проходит через точку (0,2), то есть через начальные координаты движения тела, максимальная высота подъема тела по графику составляет около 6 м (как мы уже отмечали, все расчеты ведутся в СИ), дальность полета около 2 м, что можно проверить, решив задачу аналитически в той же программе.
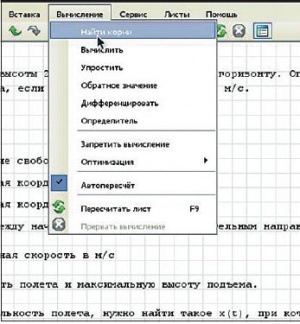
Чтобы решить уравнение, введем его основную часть (ту, что после знака равенства, содержащую переменные), выделим переменную и в меню «Вычисление» выберем «Найти корни уравнения» (рис. 12).
Анализируем полученные данные: координата начального положения тела совпадает с полученной графически, максимальная высота подъема тела также совпадает, а вот дальность полета совершенно не соответствует полученной графическим способом.
Какое-то из решений ошибочно. Чтобы выяснить, какое именно, нужно решить задачу еще одним способом. Попробуем решить систему уравнений вручную, то есть перепишем уравнение
x(t) = x0 + v0*cos(α)*t
в виде
t = (x – x0)/(v0*cos(α)).
Рис. 12. Вычисляем корни, выбрав нужный пункт.
Рис. 13. Траектория полета тела под углом к горизонту.
Затем запросим программу найти зависимость y(t) при полученном выражении для t.
Строим график 2D для полученной функции (рис. 13) и видим, что все контрольные параметры совпадают с полученными аналитическим способом данными. Делаем вывод, что программа неверно осуществила решение системы уравнений, и полученное в первом случае выражение в действительности не является решением системы. Оказывается, в SMathStudio нет специального механизма для решения систем уравнений, обычно их решают с помощью матриц. Такой способ неприменим для девятиклассников, изучающих кинематику, поэтому в дальнейшем при необходимости решения системы уравнений будем прибегать ко второму способу, давшему верный результат для данной задачи.
Такая, казалось бы, неудача – на самом деле очень ценный случай для формирования у школьников правильного отношения к решению задач с помощью любых автоматизированных систем. Любое решение необходимо проверять. Разные способы решения одной и той же задачи, а они могут заключаться даже в разных механизмах постановки запроса на решение у программы, являются надежным средством проверки.
Виртуальное моделирование имеет большую ценность для преподавания физики. Не всегда есть возможность продемонстрировать изучаемое явление. Однако не следует строить методику преподавания физики только на виртуальном эксперименте. Когда есть возможность демонстрации или самостоятельной постановки учащимися натурных физических экспериментов, ею необходимо воспользоваться. Недопустимо, чтобы наука о природе превратилась в науку о виртуальном мире. У виртуального эксперимента свое место в процессе обучения физике, и не нужно делать его царем. В то же время, очень хотелось бы, чтобы от мелового объяснения теории мы могли бы перейти к объяснению с помощью интерактивных виртуальных моделей. Программы для моделирования физических опытов, которые мы описали выше, были бы хорошим началом.
Дистрибутив EduMandriva 2010 Spring содержит еще не одну программу, позволяющую решать задачи преподавания физики. Здесь большое поле для творчества учителя и учеников. Покажите своим ученикам Linux с этими программами, в игровой форме открывающими физическую сущность явлений и процессов природы, и они проявят больше интереса к такой сложной и трудной науке, как физика.
