- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF135:Perl
Материал из Linuxformat.
- Math::FFT Perl и математические преобразования «вытянут» безнадежные с виду снимки
Perl: Повысим качество фото
| Perl Марко Фиоретти |
|---|
| Perl Михаил Смирнов |
|---|
|
- Часть 2: Большинство, наверное, возьмет для этих целей графический редактор, но Михаил Смирнов проделает все сам, с помощью Perl и изрядной доли математики.
Наиболее важной характеристикой цифровой фото- и видеотехники является разрешающая способность преобразователей света в электрический сигнал. Чем она лучше, тем более мелкие детали мы можем наблюдать в изображении. В современных бытовых цифровых фото- и видеоустройствах такими преобразователями являются полупроводниковые приборы с зарядовой связью (ПЗС), которые не так уж давно пришли на смену фотопленке и вакуумным преобразователям света. Основное преимущество ПЗС перед фотопленкой состоит в возможности регистрировать значительно больший диапазон внешней освещенности или, иначе говоря, получать значительно большее количество градаций полутонов в изображении. Преимущество перед вакуумной техникой, прежде всего, характеризуется практически стопроцентным исключением геометрических искажений. Слабым местом первых ПЗС-разработок являлось низкое оптическое разрешение, что было связано с крупным размером фоточувствительных ячеек ПЗС. Чем меньше геометрический размер ячеек и чем больше количество таких ячеек в чипе ПЗС, тем лучшее оптическое разрешение можно получить. Количество ячеек по горизонтали и вертикали определяют размер цифрового изображения в пикселях по ширине и высоте.
В первых разработках, особенно фототехники, применялась процедура искусственного увеличения количества пикселей с помощью интерполяции. Эта процедура получила название «электронного зума», применение которого может создавать только иллюзию улучшения качества изображения. Вместе с тем, такая числовая характеристика, как количество пикселей, дает лишь общее представление о качестве и реальном оптическом разрешении. Чтобы более точно разобраться в этом вопросе, нужно привлечь к рассмотрению функциональную характеристику – передаточную функцию ПЗС.
Немного теории
Рис. 1. Функция передачи модуляции камеры на ПЗС.
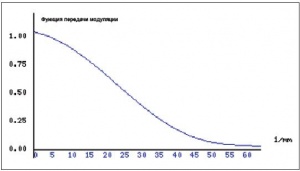
Передаточная характеристика устройства на ПЗС – сканера, цифрового фотоаппарата или видеокамеры – полностью описывается функцией передачи модуляции (ФПМ), которая характеризует падение контраста синусоидальных составляющих сигнала изображения в области пространственных частот. При оценке передаточной характеристики этих устройств одновременно будет учитываться и ФПМ оптического объектива, который фокусирует изображение в плоскости чипа ПЗС. В оптике пространственные частоты определяются как число линий на миллиметр, то есть величиной [1/мм]. В качестве примера на рис. 1 представлена типичная кривая ФПМ камеры на ПЗС.
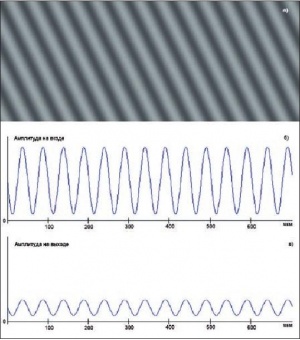
ФПМ характеризует связь между исходным объектом и его изображением. Рассмотрим в качестве объекта синусоидальное распределение контраста, показанное на рис. 2а. Частота синусоиды равна 20 1/мм, то есть на одном миллиметре укладывается 20 периодов синусоиды.
На рис. 2б и 2в представлены сечения синусоидального объекта. Размах синусоиды на рис. 2б характеризует контраст объекта на входе устройства. На выходе оптико-электронного устройства изображение синусоиды будет характеризоваться сечением, показанным на рис. 2в. Таким образом, видно, что ФПМ на частоте 20 1/мм показывает падение сигнала синусоиды с величины 1.0 на входе устройства до величины примерно 0.18 на его выходе.
Рис. 2. Пример синтеза изображения.
Рис. 3. Край полуплоскости: а) тестовое изображение края полуплоскости, б) сечение края полуплоскости, в) функция рассеяния линии, г) ФПМ устройства на ПЗС, д) дефокусировочная кривая.
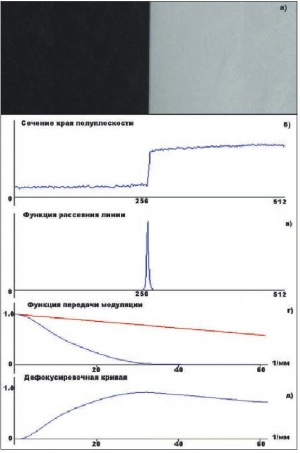
Для получения значений ФПМ на всех пространственных частотах потребуется множество синусоидальных объектов с различными частотами. Однако в этом нет необходимости, если воспользоваться объектом в виде протяженного резкого скачка контраста, получившего название «края полуплоскости». Изображение края полуплоскости показано на рис. 3а. Чтобы получить искомую ФПМ, необходимо выполнить дифференцирование края полуплоскости (по нормали к краю), а затем сделать преобразование Фурье.
Последовательность и результаты преобразований иллюстрируются на рис. 3. На рис. 3б показано одно из сечений края полуплоскости. Чтобы снизить влияние шумов ПЗС, перед дифференцированием предварительно выполняется усреднение сечений края полуплоскости. Суммирование m сечений края полуплоскости обеспечивает повышение отношения сигнал-шум в корень из m раз. Результат дифференцирования усредненного сечения края полуплоскости показан на рис. 3в – полученное нами распределение называется функцией рассеяния линии. Для определения ФПМ остается выполнить преобразование Фурье функции рассеяния и затем вычислить модуль от полученных комплексных коэффициентов Фурье (рис. 3г). Чтобы оценить ошибку, которую вносит цифровая оптико-электронная система, потребуется выполнить вычитание полученной нами ФПМ H(v) из так называемой дифракционной ФПМ Ĥ(v), которая имеет максимально достижимую частоту vm:
U(v) = Ĥ(v) – H(v)
v – пространственная частота. Предельная частота дифракционной ФПМ определяется простой формулой vm = F/λD, где F – фокусное расстояние объектива; D – диаметр объектива; λ – длина волны света, обычно принимается равной 660 нанометрам (оранжевый цвет).
Дифракционная ФПМ (красная линия на рис. 3г) представляет собой наклонную прямую, равную 1 на нулевой частоте v = 0 и равную 0 на дифракционной частоте vm. Пример разностной ФПМ U(v) показан на рис. 3д. Кривая на рис. 3д характеризует величину ошибки передачи контраста, которая обусловлена реальной оптико-электронной системой на ПЗС. Во многих случаях подобная ошибка связана с расфокусировкой объектива (потерей резкости). И действительно, распределение на рис. 3д напоминает дефокусировочную кривую.
Различные варианты настройки фокуса объектива будут, в той или иной степени, приводить к потере резкости. Чем сильнее расстроен объектив, тем больше будут значения разностной функции U(v) и тем хуже оптическое разрешение. При этом по пику кривой можно оценить пространственную частоту v, на которой ФПМ имеет наибольший градиент падения контраста. Если не при-нимать в расчет шумы камеры на ПЗС, то наибольшее разрешение оптико-электронной системы определяется соотношением vL=1/2L, где L – линейный размер ячейки ПЗС. Для реальных систем уровень шума на высоких частотах будет превышать сигнал изображения, и реальное предельное разрешение vr будет значительно ниже vL.
Пример кода для получения искомой ФПМ показан ниже. Исходная матрица изображения B(x,y) края полуплоскости содержится в двумерном массиве @B. Начальная и конечная строки суммирования задаются параметрами $row1 и $row2, соответственно.
for($j=$row1;$j<$row2; $j++){ for($i=0;$i<$N; $i++){ $g[$i] +=$B[$i][$j]; }} $Nrr=$row2-$row1-1; @g=map($_/$Nrr, @g); for($i=1;$i<$N; $i++){ $PSF[$i] = $g[$i] - $g[$i-1]; } use Math::FFT; for($i=0;$i<$N;$i++){ $data->[2*$i]=$PSF[$i]; $data->[2*$i+1]=0; } $fft = new Math::FFT($data); $coeff = $fft->cdft(); for($i=0;$i<$N;$i++){ $H[$i] = sqrt ( $coeff->[2*$i]**2 + $coeff->[2*$i+1]**2 ); } @H=map($_/$H[0], @H);
Результат дифференцирования заносится в массив @PSF, который представляет собой функцию рассеяния линии. Для выполнения преобразования Фурье воспользуемся математической библио текой Perl Math::FFT, в которой реализован алгоритм быстрого преобразования. Одномерное преобразование Фурье в этой библиотеке выполняется с помощью подпрограммы cdft().
Результат преобразования Фурье заносится в массив коэффициентов $coeff, где коэффициенты с четным индексом соответствуют реальной части, а коэффициенты с нечетным индексом – мнимой части комплексного числа, соответственно. Результирующая ФПМ заносится в массив @H, значения которого нормируются к первому значению массива $H[0], соответствующему постоянной составляющей изображения. Таким образом, $H[0]=1, а все остальные значения ФПМ меньше единицы.
На рис. 3г, вместе с вычисленной нами ФПМ, красной линией показана дифракционная оптическая функция. Таким образом, чем ближе ФПМ нашего устройства к дифракционной функции, тем с более высоким качеством мы сможем получать наши фотоизображения.
Улучшение качества
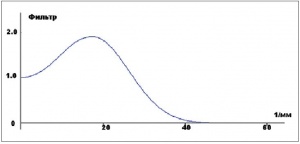
Вывод, полученный нами в предыдущем разделе, позволяет сформулировать подход для улучшения качества фотоизображений, а именно: компенсировать падение ФПМ на тех частотах, где оно выражается наиболее сильно, и приблизить тем самым ФПМ к дифракционному пределу. В цифровой обработке изображений такие восстанавливающие фильтры получили название обратных или инверсных. Математически это выражается достаточно просто, а именно: спектр исходного фотоизображения S(v) необходимо умножить на функцию, обратную ФПМ устройства на ПЗС, которую мы ранее восстановили из изображения края полуплоскости. В предположении, что мощность шума пренебрежимо мала, спектр восстановленного изображения равен отношению S1(v) = S(v)/H(v), то есть функция идеального фильтра Q(v) = 1/H(v). Принимая во внимание шумы, которые вносятся любой реальной системой, необходимо найти решение для Q(v) на тех частотах v > vr, где шум превышает сигнал. Предельная частота vr оценивается как частота, на которой дисперсия (энергия) шума начинает превышать значения ФПМ. Один из вариантов оптимального фильтра имеет вид
Рис. 4. Оптимальный линейный фильтр для улучшения фотоизображений.
Q(v)= [1 + H(vr)2]•H(v)/[H(vr)2 + H(v)2] (1)
На рис. 4 показан результат расчета фильтра по формуле (1). Инверсные оптимальные фильтры, использующие восстановленные ФПМ, обеспечивают повышение контрастности на тех пространственных частотах, на которых это падение обусловлено реальной оптико-электронной системой. Это основное отличие восстанавливающих фильтров от «слепых» фильтров высоких частот или операторов типа Собеля для подчеркивания границ, применяемых в распространенных программных пакетах.
Алгоритм улучшения качества фотоизображения с помощью инверсной фильтрации включает следующие этапы. На первом этапе осуществляется преобразование Фурье исходного фотоизображения B(x,y) и получение спектра S(vx,vy). На втором этапе формируется инверсный фильтр Q(vx,vy), значения которого умножаются на спектр S(vx,vy). На третьем этапе выполняется обратное преобразование Фурье произведения S1(vx,vy) = S(vx,vy)•Q(vx,vy), результатом которого будет являться восстановленное изображение B1(x,y).
Первый и третий этапы реализуются с помощью стандартных подпрограмм одномерного преобразования Фурье модуля Perl Math::FFT. Двумерное преобразование Фурье получается с помощью последовательного применения одномерного преобразования, например, к функции изображения B(x,y) сначала по строкам, а затем по столбцам матрицы. Отметим, что преобразованию подвергаются RGB-компоненты цветного изображения по отдельности. В наших примерах используется компонента Blue исходного RGB-изображения. Ключевым этапом преобразования является второй этап, обеспечивающий развертывание одномерной функции фильтра в двумерный массив и умножение значений фильтра на спектр исходного изображения. Фрагмент программной реализации такого алгоритма фильтрации представлен ниже:
$N2=$N/2; for($i=0;$i<$N2;$i++) { $FILTER[$i] = (1.+ $MTF[$nf]**2)*$MTF[$i]/($MTF[$nf]**2 + $MTF[$i]**2); } for($j=0;$j<$N; $j++){ for($i=0;$i<$N; $i++){ $w2[$i][$j]=0; }} &d2cdft(\@B,\@w2,\$N,\$PI); for($k=0;$k<$N; $k++){ $k1=$k; if($k > $N2) { $k1=$k-$N;} $x=$k1**2; for($j=0;$j<$N; $j++){ $j1=$j; if($j > $N2) { $j1=$j-$N;} $R = sqrt ( $x +$j1**2 ); $Q = &parv(\$R,\@Xc,\@FILTER,\$N2); $Re[$k][$j] *=$Q; $Im[$k][$j] *=$Q; }} &d2cdfti(\@Re,\@Im,\$N,\$PI);
Входное фотоизображение содержится в двумерном массиве @B. Прямое и обратное двумерное преобразование Фурье выполняются с помощью подпрограмм d2cdft() и d2cdfti(), соответственно. Исходная функция ФПМ, полученная нами выше, находится в массиве @MTF. Функция фильтра, рассчитанная по формуле (1), заносится в одномерный массив @FILTER. Для получения двумерной функции фильтра Q(vx,vy) используется подпрограмма линейной интерполяции parv(), которая обеспечивает вычисление промежуточных значений фильтра в плоскости пространственныхчастот (vx,vy). Параметр R является текущим радиусом, а вспомогательный массив @Xc представляет собой массив аргумента входной функции фильтра, и, в частности, может быть задан как безразмерная функция с единичным шагом:
for($j=0;$j<$N2; $j++){$Xc[$j]=$j;}
Выходные значения восстановленного спектра S1 фотоизображения заносятся в массивы реальной @Re и мнимой @Im части комплексного спектра S1, соответственно. Результирующее восстановленное изображение, после выполнения обратного преобразования Фурье с помощью подпрограммы d2cdfti(), помещается в двумерный массив @Re. На рис. 5 показано исходное и восстановленное фотоизображения, полученные с помощью цифровой фотокамеры в стандартном режиме съемки.
Рис. 5. Результат компенсации ФПМ фотокамеры для стандартного режима съемки: а) исходное фотоизображение (Blue), б) результат восстановления.
Рис. 6. Результат компенсации ФПМ фотокамеры для режима съемки макро: а) исходное фотоизображение (Blue), б) результат восстановления.
Как правило, в этом режиме съемки цифровые фотографии получаются вполне удовлетворительного качества. Чаще всего пониженное качество цифрового фото связано с режимом макросъемки. На рис. 6 показано исходное и восстановленное фотоизображения, которые были получены в этом режиме.
С точки зрения нагрузки на процессор, при выполнении процедур улучшения качества наиболее затратной является процедура интерполяции. Для уменьшения времени обработки фотоизображения можно заранее сформировать двумерную матрицу фильтра Q(vx,vy) и хранить его на диске. Для перемножения матриц спектра исходного фотоизображения S(vx,vy) и матрицы фильтра Q(vx,vy) можно воспользоваться пакетом (модулем) Perl PDL. Основное достоинство пакета PDL – высокая скорость сложения и перемножения матриц большой размерности и компактное хранение массивов данных с плавающей запятой. Например, скалярное произведение двух матриц вещественных чисел с плавающей запятой и размерностью 2048 × 2048 составляет около 1 секунды, а сложение таких матриц займет доли секунды. Двумерный массив чисел с плавающей запятой размерностью 1024 × 1024, принимая тип данных PDL, будет занимать всего 4 МБ оперативной памяти. Пакет PDL позволяет лаконично записывать математические операторы для работы с матрицами в виде одной строки – например, код для скалярного умножения двух матриц $a и $b будет иметь вид
use PDL; $c = $a * $b;
Соответственно, код для перемножения двумерного комплексного спектра изображения на двумерный фильтр запишется в виде
$re = pdl[@Re]; $im = pdl[@Im]; $q = pdl[@Q]; $re = $q*$re; $im = $q*$im;
Уважаемый читатель, если вас поначалу озадачили «преобразование Фурье» и реализация математических формул, то отнеситесь к ним как к «черному ящику». Главная польза применения Math::FFT для оценки качества состоит в том, что с помощью небольшой программы на Perl у вас появилась возможность объективно сравнивать оптическое разрешение современных фото- и видеосистем во всей полосе видеочастот, а не ориентироваться только на один параметр разрешения – количество мегапикселей.
