- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF134:OLAP
Материал из Linuxformat.
- Многомерный анализ Разбор реальной программы, выявляющей закономерности
Содержание[убрать] |
OLAP: Анализ данных и СПО
- Выложить белый хлеб по соседству с молоком или колбасой? Ответ на этот вопрос поможет найти многомерный анализ данных, а Вячеслав Олоничев и Андрей Сенов реализуют его на Qt и C++.
Многомерный анализ данных или OLAP – это технология, интуитивно понятная любому, кто когда-либо занимался обобщением данных по продажам, выпуску продукции и тому подобным. Эта технология востребована практически повсеместно, начиная от маленькой мастерской или фермерского хозяйства и заканчивая министерством или центральным офисом транснациональной корпорации. Соответственно, и решений для нее существует достаточно много. Здесь можно найти и нестандартные расширения SQL типа pivot в Access, подключаемые модули для электронных таблиц или той же «1С», превеликое множество программ на Delphi с его Decision Cube или VBA, и, наконец, инструментарий для многомерного анализа на стороне сервера от Microsoft или Oracle. Наиболее удобные и продвинутые решения в данной области предназначены в первую очередь для больших корпораций и имеют соответствующую стоимость. Использование же электронных таблиц крайне трудоемко и неэффективно. И кроме того, все указанные решения являются проприетарными.
Описываемая здесь программа (вы найдете ее полные исходные тексты на LXFDVD) отличается от имеющихся в первую очередь тем, что использует только свободный код и сама является открытой. Предназначена она для многомерного анализа данных на стороне клиента, что и определяет область ее потенциального применения: небольшие и средние предприятия, для которых SQL-запрос, отбирающий данные за пять-шесть лет, будет выполнен на сервере и передан по локальной сети клиенту за приемлемое время.
Программа основана на выполнении всех операций по многомерному анализу с использованием типовых структур данных в ОЗУ, что должно обеспечить достаточно высокую эффективность при умеренных затратах памяти. Наиболее полная, удобная и эффективная реализация типовых структур данных – это параметризованные контейнеры на языке С++, такие как стандартная библиотека шаблонов STL и библиотека шаблонов Qt.
Как контейнеры STL, так и контейнеры Qt – это свободное ПО. Разница между ними настолько мала, что фрагменты исходного кода, содержащие обращение к STL, можно переделать в код, работающий с шаблонами Qt (и наоборот), буквально за пару минут.
В нашем случае используются шаблоны Qt, по следующей причине: поскольку графический интерфейс программы выполнен с использованием библиотеки Qt и доступ к базе данных производится также средствами Qt, то шаблоны Qt следует применять не только из принципа единообразия, но и ради эффективности, так как они тесно взаимодействуют с основной библиотекой. Модуль многомерного анализа в программе выделен в отдельный класс, поэтому его легко адаптировать к другой платформе или библиотеке. Кстати говоря, первая версия программы была выполнена на C++ Builder с использованием STL, потом интерфейс был переписан на Qt3 в KDevelop, но STL сохранена. А текущая реализация выполнена на Qt4 в среде Qt Creator.
Для многомерного анализа данных на стороне клиента требуется решить следующие задачи:
- Выбор структуры данных для сохранения в ОЗУ результатов SQL-запроса и требования к тексту SQL-запроса.
- Формат представления выбранных осей гиперкуба для формирования его проекции на плоскость.
- Формирование самой проекции.
- Формирование итогов.
При решении данных задач будем последовательно придерживаться принципа повсеместно использовать параметризованные контейнеры. Это стремление не столько к соблюдению единого стиля, сколько к эффективности, так как позволяет свести к минимуму все if-else’ы и switch-case’ы и максимально использовать оптимизированный код параметризованных контейнеров.
STL и OLAP
Прежде чем углубляться в детали, разъясним несколько терминов. Стандартная библиотека шаблонов (Standard Template Library, STL) – набор согласованных обобщенных алгоритмов, контейнеров, средств доступа к их содержимому и различных вспомогательных функций (http://ru.wikipedia.org/wiki/Стандартная_бибилотека_шаблонов).
OLAP (On Line Analytical Processing – интерактивная аналитическая обработка данных) – один из способов представления и анализа данных. При этом информация представляется в виде многомерного куба с возможностью произвольного манипулирования ею. Многомерные модели рассматривают данные либо как факты с соответствующими численными параметрами, либо как текстовые измерения, которые характеризуют эти факты. (Каширин И.Ю., Семченков С.Ю. Интерактивная аналитическая обработка данных в современных OLAP системах // Бизнес-информатика – 2009. – № 2. С.12–19. См. также http://ru.wikipedia.org/wiki/OLAP).
Выбор структуры данных
SQL-запрос, поставляющий данные для многомерного анализа, должен иметь вид:
SELECT ось0, ось1, ... осьN, val FROM ... INNER JOIN ... ON ... ... WHERE some_date BETWEEN :d1 AND :d2
где ось0, ось1, …, осьN – результаты измерений на осях гиперкуба; val – анализируемое значение, содержащееся в ячейке гиперкуба; :d1,:d2 – параметры, задающие интервал времени, за который производится анализ.
Запрос возвращает реляционную таблицу, в которой атрибуты, соответствующие результатам измерений, могут иметь самые разнообразные типы, а последний атрибут – val – практически всегда является числом с плавающей точкой.
Наша задача – реализовать не только универсальный способ сохранения результатов в ОЗУ, но и обеспечить возможность построения как простых, так и составных ключей по результатам измерений на осях гиперкуба, которые будут необходимы как для упорядочивания, так и для поиска информации. Поэтому все результаты измерений следует привести к одному типу в самом начале, еще до размещения в ОЗУ. В качестве такого типа был выбран строковый. Это объясняется тем, что большинство атрибутов, соответствующих результатам измерений на осях гиперкуба, изначально имеют строковый тип – это наименования товаров, предприятий, фамилии работников и тому подобное. Все другие типы всегда можно преобразовать к строковому. Что касается дат, то если их преобразовать в строковый вид при помощи SQL-функции cast в так называемом армейском формате – «гггг.мм.дд» – то упорядочивание строк в алфавитном порядке будет соответствовать упорядочиванию дат в порядке возрастания.
Таким образом получаем:
typedef QVector<QString> s_keys; struct l_cube{ s_keys dims; double r; }; typedef QVector<l_cube> data_cube;
где s_keys – вектор, в который помещаются результаты измерений; l_cube – структура для сохранения одной строки, возвращаемой запросом; data_cube – вектор, для сохранения в ОЗУ таблицы, возвращаемой запросом.
Закачка информации в память, если смотреть изнутри, осуществляется следующим образом:
class hyper_cube{ protected: data_cube dc; l_cube line; ... public: void add(s_keys sk, double res){ line.r = res; for(int i=0; i<N; i++) line.dims[i]=sk[i]; dc.push_back(line); } ... }
А снару жи это выглядит так:
hyper_cube HC; s_keys VK; QSqlQuery* psql; QDate d1,d2; psql>bindValue(“:d1”,QVariant(d1)); psql>bindValue(“:d2”,QVariant(d2)); if(psql>exec()){ while ( psql>next() ) { for(int i=0; i<Nax; i++){ VK[i] = psql>value(i).toString() + '\n'; } HC.add(VK, psql>value(Nax).toDouble()); } }
Здесь Nax – количество осей гиперкуба. Если использовать однонаправленный запрос, то приведенный код будет достаточно эффективным.
База данных
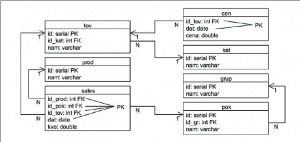
В качестве примера используем фрагмент базы данных предприятия, занимающегося мелкооптовой продажей столовой посуды. База данных реализована на SQLite (каталог primer в исходных текстах программы), а ее ER-диаграмма представлена на рис. 1.
В указанной базе данных имеются следующие таблицы: kat – категории товара, tov – товары, prod – продавцы, grup – группы покупателей, pok – покупатели; cen – цены на товары, sales – продажи.
Следующий запрос возвратит гиперкуб с данными о продажах в рублях, содержащий 8 осей:
SELECT k.nam, t.nam, pr.nam, g.nam, pk.nam, substr(cast(s.dat AS char(32)),1,4) AS ye, substr(cast(s.dat AS char(32)),1,7) AS mo, substr(cast(s.dat AS char(32)),1,10) AS da, s.kvo*c.cena AS sum FROM sales s INNER JOIN cen c ON c.id_tov=s.id_tov INNER JOIN tov t ON t.id=s.id_tov INNER JOIN prod pr ON pr.id=s.id_prod INNER JOIN pok pk ON pk.id=s.id_pok INNER JOIN grup g ON g.id=pk.id_gr INNER JOIN kat k ON k.id=t.id_kat WHERE c.dat=(SELECT max(dat) FROM cen WHERE cen.id_tov=s.id_tov AND dat<=s.dat) AND s.dat BETWEEN :d1 AND :d2
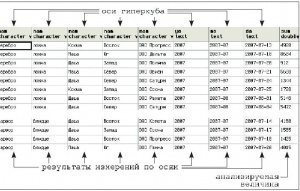
Осями гиперкуба в данном случае являются: 0 – категория, 1 – товар, 2 – продавец, 3 – группа, 4 – покупатель, 5 – год, 6 – месяц, 7 – день. Фрагмент гиперкуба или таблицы, полученной в результате выполнения данного запроса, можно видеть на рис. 2.
Формат представления
Следующая проблема – выбор пользователем осей гиперкуба для формирования проекции и передача этой информации коду, который и будет ее формировать. Для пользователя естественным представлением осей гиперкуба являются два списка, один для оси X проекции и второй – для оси Y, допускающих множественный выбор и перемещение элементов списка относительно друг друга. Эти два требования являются обязательными; программа, не отвечающая им, не представляет большого интереса для практики.
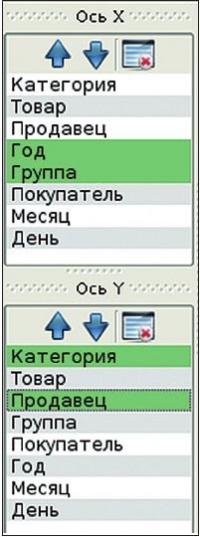
Для приложения использование наименований осей не совсем удобно – предпочтительней использовать номера: ведь данные измерений хранятся в векторах, и индекс в векторе однозначно соответствует номеру оси. Поскольку элементы списка могут изменять взаимное расположение, то их текущие номера уже не будут соответствовать номерам осей гиперкуба. Для решения данной задачи воспользуемся словарем QMap<QString, int>, который позволит по выбранной пользователем строке с названием оси определить ее номер. Допустим, что, как представлено на рис. 3, пользователь решил проанализировать, как распределяются продажи по годам и группам покупателей, с одной стороны, и по категориям товаров и продавцам, с другой. Для этого ему пришлось переместить ось гиперкуба «Год» вверх по списку для проекции на ось X – ведь его интересует распределение продаж по группам покупателей в пределах каждого года; иначе у него получилось бы распределение продаж по годам в пределах каждой группы. Определим следующие переменные: myAxes – массив QVector<QString>, содержащий наименования осей гиперкуба; lstX и lstY – списки QListWidget, пред-назначенные для отображения и выбора осей гиперкуба для осей X и Y проекции; m_axe – словарь QMap<QString,int>, позволяющий получить порядковые номера по наименованиям осей гиперкуба; xJ, yI – массивы QVector<int>, содержащие номера осей гиперкуба, отобранные для отображения на оси X и Y проекции. В результате, в примере на рис. 3, массив xJ будет содержать числа 5 и 3, а массив yI – числа 0 и 2.
Формирование проекции
При формировании отчета будем использовать следующие правила: в ячейки проекции помещаются только суммы, а итоги могут содержать или суммы, или средние, или минимумы/максимумы значений, содержащихся в клетках проекции, в зависимости от выбора пользователя. Таким образом, при выборе максимума мы будем получать максимальную сумму продаж категории товаров продавцом каждой группе потребителей за год, а не максимальную единичную продажу.
Как проекцию, так и итоги будем помещать в двумерный массив чисел с плавающей точкой. Значения измерения по осям «пририсовываются» к отчету на последнем этапе, когда он отображается в QTableWidget в окне диалога. Размер данного двумерного массива известен на момент формирования, и поэтому можно использовать обычный динамический массив. Однако, просто из принципа единообразия, будем использовать тип данных Qvector<QVector<double>>.
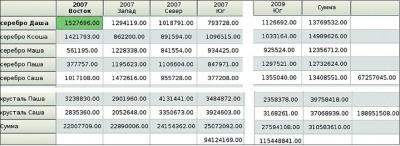
На рис. 4 представлен фрагмент проекции и итогов; заголовки колонок таблицы содержат результаты измерений по осям гиперкуба – «Год» и «Группа предприятий», которые отражены на ось X проекции. В клетках проекции представлены суммы продаж, распределенные по годам и группам предприятий, с одной стороны, и категориям товаров и продавцам, с другой стороны. Итоги внизу представляют суммы по годам и группам предприятий. Строчка ниже содержит суммы продаж по годам, а самая правая колонка – суммы продаж по категориям товаров.
Задача заключается в том, чтобы выбрать из таблицы с результатами запроса уникальные сочетания измеренных значений на выбранных осях гиперкуба и упорядочить их в алфавитном порядке. А затем следует отобрать значения анализируемой величины, в данном случае – суммы продаж, из соответствующих строчек таблицы и просуммировать их в нужных клетках проекции. Для решения задачи будем использовать словарь QMap<QString, int>.
В данном фрагменте кода сканируется таблица dc, содержащая результаты запроса к базе данных, как показано на рис. 2. Векторы xJ и yI, как уже было сказано, содержат номера выбранных осей, {5, 3} и {0, 2} соответственно. В ходе выполнения цикла строка xs будет последовательно принимать значения «2007\nВосток\n», «2007\nЮг\n», «2007\nЗапад\n», «2007\nСеверг\n» и т. д., а строка ys – «серебро\nКсюша\n», «серебро\nМаша\n», «серебро\nДаша\n», «серебро\nМаша\n» и т. д. И все эти строки, являющиеся полными составными ключами для осей X и Y проекции гиперкуба, будут помещаться как ключи в словари pX и pY. Значения, помещаемые в словари, на данном этапе не важны, и поэтому для них используется -1. Словарь может содержать только неповторяющиеся ключи, поэтому по завершении цикла словари pX и pY будут содержать все уникальные значения полных составных ключей, содержащихся в таблице с данными.
QString xs, ys; Qmap<QString,int> pX,pY; int Hx=xJ.size(); int Hy=yI.size(); for(int i=0; i<dc.size(); i++){ xs=””; ys=””; for(int x=0; x<Hx; x++) xs=xs+dc[i].dims[xJ[x]]; for(int y=0; y<Hy; y++) ys=ys+dc[i].dims[yI[y]]; (*pY)[ys]=1; (*pX)[xs]=1; }
Следующий фрагмент кода перебирает все ключи, содержащиеся в словарях pX и pY, при помощи итератора, и присваивает им монотонно возрастающие целочисленные значения. В результате наши словари содержат в качестве ключей наименования строк и колонок проекции, а в качестве значений – номера соответствующих строк и колонок. Это как раз то, что и требуется для заполнения ячеек проекции.
Qmap<QString,int>::iterator it; int m,n; m=0; for(it=(*pY).begin(); it!=(*pY).end(); it++) {it.value()=m++;} n=0; for(it=(*pX).begin(); it!=(*pX).end(); it++) {it.value()=n++;}
В нижеследующем цикле значения полных составных ключей опять восстанавливаются из значений измерений, а по ним определяются координаты ячейки проекции, к содержимому которой добавляется значение анализируемой величины из очередной строчки сканируемой таблицы с результатами запроса.
int I,J; for(int i=0; i<dc.size(); i++){ xs=””; ys=””; for(int x=0; x<Hx; x++) xs=xs+dc[i].dims[xJ[x]]; for(int y=0; y<Hy; y++) ys=ys+dc[i].dims[yI[y]]; I = (*pY)[ys]; J = (*pX)[xs]; dp[I][J]+=dc[i].r; }
Формирование итогов
Осталась последняя проблема – формирование итогов по полным и частичным ключам. Как уже было сказано выше, надо получить суммы продаж, распределенные по группам потребителей в пределах года, а также суммы продаж по годам. Так вот, «Год\nГруппа_компаний\n» – это полный ключ, имеющий уникальное значение для каждой колонки проекции, а «Год\n» – это частичный ключ. Если построить словари с частичными ключами, то можно определить как координаты ячеек в итогах, «пристроенных» к проекции справа и снизу, так и расстояние между этими координатами – то есть количество ячеек в итогах, определенных по полным ключам, которые необходимо использовать для формирования итогов по частичным ключам. Поскольку количество осей гиперкуба, накладываемых на ось проекции, может быть произвольным, то для формирования частичных ключей будем использовать вектор словарей: QVector<QMap<QString,int>>.
Формирование итогов будем осуществлять при помощи циклов, перебирающих ячейки массива с проекцией гиперкуба. А проблему вида итогов, а именно: сумма, среднее, максимум или минимум – будем решать при помощи виртуальных функций вспомогательных классов.
class Ttl{ protected: double r; public: void setR(double R); virtual void updR(double E)=0; virtual double getR(int N)=0; }; class Sum: public Ttl{ public: virtual void updR(double E); virtual double getR(int N); }; class Avg: public Sum{ public: virtual double getR(int N); }; class Max: public Sum{ public: virtual void updR(double E); }; class Min: public Sum{ public: virtual void updR(double E); }; void Ttl::setR(double R){r=R;} void Sum::updR(double E){r+=E;} void Max::updR(double E){if(E>r)r=E;} void Min::updR(double E){if(E<r)r=E;} double Sum::getR(int N){return r;} double Avg::getR(int N){return r/N;}
Имена у классов говорящие, а предназначение функций очевидно и не требует разъяснений. Единственное, что вызывает вопрос, так это виртуальные функции. Стоило ли бороться за эффективность кода, используя параметризованные контейнеры, чтобы потом все, сэкономленное буквально по миллисекундам, так бездарно спустить в последний момент? Поясним: параметризованные контейнеры используются внутри циклов, сканирующих таблицу с исходными данными или гиперкуб. Данная таблица в реальных задачах может иметь несколько десятков, а то и сотен тысяч строк. А для массива, в котором формируется проекция и итоги, счет идет на десятки. Теоретически, конечно, можно сформировать отчет и на несколько тысяч строчек и колонок, только кто же его смотреть будет?
Финальные штрихи
Вывод проекции и итогов на форму и добавление к ним заголовков строк и столбцов – самостоятельная задача, и в данной статье не рассматривается, наряду с остальными вопросами проектирования интерфейса с пользователем, а также формата файла, в который помещается отчет, сгенерированный программой. Но в программе, которую (напомним) вы найдете на LXFDVD, все это сделано. Поэтому она готова к использованию «из коробки».
Предлагаемая методика многомерного анализа данных, конечно, не ограничивается только языком C++ и библиотекой Qt. Вполне возможна реализация на wxWidgets с использованием STL, а параметризированные шаблоны имеются и в языках Java и C#.
В последний момент, просматривая демонстрационную базу данных, мы заметили, что девушки-продавщицы проработали у нас по три года без отпусков. Да... Лучше бы мы взломали базу данных сиротского приюта.