- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF133:Python
Материал из Linuxformat.
Python Реальные проекты, оттачивающие навыки хакера
Содержание |
Python: Кох и его снежинка
- Ник Вейч упражняется в математике, сочетая теорему Пифагора, Python, Clutter и Cogls и получая на выходе красивые пушистые снежинки Коха.
| Python |
|---|
| Python для профессионалов |
|---|
| Python + PyGame |
|---|
| Python + Web |
|---|
| Python + Clutter |
|---|
В прошлых выпусках этой серии мы развлекались с актерами [actor] и сценами [scene], подключив мощь дополнительных библиотек типа GStreamer и Cairo, чтобы создать побольше объектов и двигать ими, пока они не запросят пощады. Теперь пора опять заняться актерами, но на сей раз мы не ограничимся нудными прямоугольниками и текстом, предоставляемыми Clutter – нет, мы создадим свои. Для этого потребуется привлечь некоторые из примитивных методов для управления лежащими в их основе GL-объектами – порезвимся с Cogls.
Прежде чем начать, определимся с формой, которую примет наш актер. Честно говоря, основные евклидовы формы хоть и полезны, но унылы – давайте создадим нечто поинтереснее: снежинку Коха!
Что нам надо
Очевидно, прежде чем начать, надо обзавестись Python’ом и его модулем Clutter. Оба они доступны в репозиториях вашего дистрибутива, если ваш дистрибутив обновлялся хоть раз за последний год. Обычно безопаснее взять пакет оттуда; ну, а самый новый исходный код для Clutter – на сайте http://www.clutter-project.org.
Да будет снег!
Снежинка (или кривая) Коха – это вид фрактала. Строятся фракталы, как правило, процедурным способом, который на-ура адаптируется компьютерами. Уверен, что попытки построить подобные штуки несколькими строками на языке Basic, Pascal или чему там сейчас детей учат (в мое время это были Algol и Fortran) заняли немало уроков информатики.
Основная концепция проста. Берется равносторонний треугольник. Затем посреди каждой стороны строится еще по одному равностороннему треугольнику, со стороной втрое меньше, чем у исходного. Этот шаг повторяется до тех пор, пока не надоест. На рисунке показано, что получается после нескольких итераций.
По некой причине эта задача обычно решается применением рекурсивного алгоритма, вызывающего самого себя. Оно, конечно, умно и изящно, но далеко от идеала. Мало того, что алгоритм труден в понимании; он еще и ужасно прожорлив. К тому же можно наткнуться на лимит количества рекурсий: Python корежит при мысли о добавлении в стек лишнего обращения к функции. По умолчанию Python разрешает только 1000 уровней рекурсии, и хотя установкой значений системных переменных предел можно расширить, отдельные платформы задают жесткое ограничение.
Для нашего алгоритма Коха мы возьмем менее эффектный, но более эффективный подход – надежный и дружелюбный к процессору (важность этого проявится позже). Попросту, мы начнем со списка из трех точек, которые образуют более-менее правильный треугольник. В цикле будем просматривать список и вставлять три точки между каждой парой точек (не забывая про пару, состоящую из первой и последней точек). Таким образом, каждый проход цикла формирует новый уровень фрактала. Это просто, и примерно наполовину быстрее рекурсивного решения:
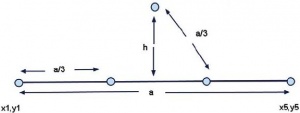
def generatekoch(depth=4): sqrtof3=1.7320508075688772 pointlist=[(0,50),(75,180),(150,50)] # более-менее равносторонний треугольник for i in range(depth): newlist=[] for p in range(len(pointlist)): x1=pointlist[p][0] y1=pointlist[p][1] if p==len(pointlist)-1: x5=pointlist[0][0] y5=pointlist[0][1] else: x5=pointlist[p+1][0] y5=pointlist[p+1][1] dx=x5-x1 dy=y5-y1 x2=x1+(dx/3.0) y2=y1+(dy/3.0) x4=x1+(2*dx/3.0) y4=y1+(2*dy/3.0) x3=(x1+x5)/2 + (sqrtof3 * (y1-y5))/6 #см. диаграмму y3=(y1+y5)/2 + (sqrtof3 * (x5-x1))/6 newlist.append((x1,y1)) newlist.append((x2,y2)) newlist.append((x3,y3)) newlist.append((x4,y4)) #точка 5 уже в списке pointlist = newlist return pointlist if __name__ == “__main__”: list=generatekoch(3) print list
Переменные внутри цикла соответствуют пяти точкам на новых отрезках. Первая и последняя – это те, что берутся из исходного списка. Остальные три надо вычислить. Вторая и четвертая лежат на одной трети и двух третях отрезка, соединяющего исходные точки, и их координаты найти несложно. Третья точка – вершина нового треугольника, которую надо вычислить. К счастью, теорема Пифагора для равносторонних треугольников весьма упрощается, и все, что нужно вычислить – это квадратный корень из 3; его можно стянуть из библиотеки math (можете и сами написать подходящее приближение). Если вас интересует математика, вспомните, что правильный треугольник – это два прямоугольных треугольника, приставленных друг к другу. За детальной картиной обратитесь к диаграмме.
Здесь мы использовали в качестве итератора цикл for, а не список: так проще работать с парой элементов. Мы формируем новый список точек, а не вставляем точки в старый, поскольку при этом, кроме всего прочего, портится счетчик цикла.
При такой генерации снежинки есть небольшой подводный камень: формулы предполагают, что точки исходного цикла расположены по часовой стрелке, иначе кривая будет вогнутой (при этом тоже, кстати, получается красивый рисунок).
Создание актеров
Теперь мы знаем, что собрались рисовать, и можно начинать строить актера. В Clutter есть метакласс для актеров, и мы используем его как шаблон. То есть, ничего не заполняя, можно сделать новый класс на основе clutter.Actor, и он уже унаследует множество методов и свойств.
Объекты Clutter и сами унаследованы от GObject, который является частью GLib от Gnome Foundation, обширной библиотеки кросс-платформенных структур данных (не путайте ее с Glibc!). Это понадобится нам в дальнейшем – мы прихватим несколько кусков из GLib, чтобы наш код заработал. А пока просто построим актера-треугольника. Откройте терминал, введите python для запуска Python в интерактивном режиме, и введите следующее (если вам лень, скопируйте и вставьте содержимое листинга с LXFDVD):
>>> import gobject >>> import clutter >>> from clutter import cogl >>> class Triangle (clutter.Actor): ... def __init__ (self): ... clutter.Actor.__init__(self) ... self._color = clutter.Color(255,255,255,255) ... def do_paint (self): ... (x1, y1, x2, y2) = self.get_allocation_box() ... width=x2-x1 ... height=y2-y1 ... cogl.path_move_to(width / 2, 0) ... cogl.path_line_to(width, height) ... cogl.path_line_to(0, height) ... cogl.path_line_to(width / 2, 0) ... cogl.path_close() ... cogl.set_source_color(self._color) ... cogl.path_fill() ... >>> gobject.type_register(Triangle) <class ‘__main__.Triangle’> >>>
Вместе с библиотекой Clutter мы также импортировали gobject и, особенно, библиотеку cogl. Последняя просто укоротит пространство имен (вместо того, чтобы писать clutter.cogl.path_move_to, можно опустить первый clutter). GObject необходим не только для добавления свойств и сигналов, но также для регистрации типа объекта, которая требуется в Clutter. Можно видеть, что мы сделали это сразу после создания класса – это необходимо произвести до создания каких-либо элементов Triangle.
В самом классе мы определили, как обычно, метод __init__. Метакласс Actor имеет свой метод init, но мы перезаписали его, чтобы добавить новую функциональность (в нашем случае это просто установка переменной цвета). Однако мы все-таки можем вызвать имевшийся по умолчанию метод __init__, явным образом; так мы свалим на Clutter ряд обычных для него вещей, с которыми нам неохота возиться самим.
Метод paint очень важен: он-то и использует функции из Cogl. Каждый актер имеет метод paint, который вызывается всякий раз, когда нужно отрисовать объект. Этот метод вызывается самим Clutter, и может вызываться множество раз, например, при анимации.
Команды рисования прозрачны для понимания. Представьте, что у вас есть перо – его нужно поместить в начальную позицию, а затем вести линии к разным точкам. Метод path_close объединяет первую и последнюю точки для замыкания контура, что обязательно при заливке. Дополнительных команд рисования полно (у многих есть абсолютные и относительные версии), и документация для примитивов доступна на сайте Clutter: http://clutter-project.org/docs/cogl/stable/cogl-Primitives.html. Конечно, это документация для C, но разобраться в работе методов там совсем несложно.
Чудеса рисования
И последний магический трюк в этом коде – в начале метода paint. Вызов get_allocation_box использует один из унаследованных методов Actor, чтобы узнать размер отрисованнного актера, который возвращает две точки, задающие пределы области рисования. На данный момент не стоит беспокоиться о размере объекта – при каждом вызове актерского метода set_size(), разнообразные внутренние процедуры Clutter позаботятся об изменении размера актера, а размер области для рисования поменяется в соответствии с ним.
Теперь протестируем наши треугольники, выполнив обычную установку сцены и добавив объекты:
>>> stage=clutter.Stage() >>> stage.set_size(400,400) >>> t=Triangle() >>> t.set_size(50,50) >>> stage.add(t) >>> stage.set_color(clutter.Color(0,0,0,255)) >>> stage.show_all() >>> tt=Triangle() >>> tt.set_size(100,100) >>> tt.set_position(200,200) >>> stage.add(tt)
Теперь можно создавать треугольники и даже анимировать их:
>>> tt.animate(clutter.EASE_IN_QUAD,2000,’y’,0) <clutter.Animation object at 0x97b334c (ClutterAnimation at 0x98a1990)>
Но не все так просто, как кажется. Попробуем поменять цвет нашего треугольника, таким способом:
>>> tt.set_color(clutter.Color(255,255,0,255)) Traceback (most recent call last): File “<stdin>”, line 1, in <module> AttributeError: ‘Triangle’ object has no attribute ‘set_color’
Налог на наследство
Функциональность стандартного актера наследуется не полностью. В отличие от встроенного объекта rectangle, у нас нет метода для установки цвета созданного нами объекта Triangle. Для этого нужно добавить в класс:
def set_color (self, color): self._color = color
Этот кусок кода, очевидно, должен быть частью главного класса, и в этом примере он принимает стандартный объект clutter.Color(), хотя это можно изменить. Так,применяя это к нашей снежинке Коха, мы получим нечто вроде следующего (заметьте, что для краткости здесь генератор Коха не показан):
import gobject import clutter from clutter import cogl class Koch (clutter.Actor): “”” Актер снежинки Коха имеет дополнительное свойство ‘_iterations’, управляющее глубиной фрактала “”” __gtype_name__ = ‘Koch’ def __init__ (self): clutter.Actor.__init__(self) self._color = clutter.Color(255,255,255,255) self._iterations = 2 self._points=[(0,0),(0,0),(0,0)] def generatekoch(self,dimension): ### см. выше return pointlist def set_color (self, color): self._color = color def __paint_shape (self, paint_color): pointlist=self._points cogl.path_move_to(pointlist[0][0], pointlist[0][1]) for point in pointlist: cogl.path_line_to(point[0], point[1]) cogl.path_close() cogl.set_source_color(paint_color) cogl.path_fill() def do_paint (self): paint_color = self._color real_alpha = self.get_paint_opacity() * paint_color.alpha / 255 paint_color.alpha = real_alpha self.__paint_shape(paint_color) def set_size (self,width,height): clutter.Actor.set_size(self,width,height) dimension=float(min(width,height)) self._points=self.generatekoch(dimension) def set_iterations (self,number): self._iterations=number (x,y) = self.get_size() dimension = min(x,y) self._points=self.generatekoch(dimension) self.do_paint() gobject.type_register(Koch)
Здесь можно видеть, что мы храним список точек в виде свойства – перерисовывать кривую глубины восемь и выше с нуля, да еще и несколько раз в секунду, было бы очень затратно! Генерация списка вызывается всякий раз, когда изменяется число итераций. Это значит, что обычно при установке объекта точки формируются дважды, предполагая, что количество итераций, стоящее по умолчанию, изменено. К сожалению, это не устранить, если только вы не хотите, чтобы «глубина» фрактала имела действие только при изменении размера.
Мы перезаписали метод set_size класса Actor, чтобы убедиться, что в сформированных нами точках отражается размер объекта, но, тем не менее, все еще необходимо вызывать метод set_size родительского класса, чтобы удостовериться, что буферы и прочее обновились.
Чтобы продемонстрировать наши новые фигуры, вот вам простой генератор для тестирования:
import clutter, random from clutterKoch import Koch stage = clutter.Stage() stage.set_size(640, 480) stage.set_color(clutter.Color(0,0,0,255)) stage.connect(‘destroy’, clutter.main_quit) for i in range(10): s = Koch() x=random.randint(20,90) s.set_size(x, x) s.set_iterations(6) s.set_color(clutter.Color(200,200,random.randint(200,255),255)) z=random.randint(0+x,640-x) zz=random.randint(x,x+200) s.set_position(z,-zz) stage.add(s) s.animate(clutter.EASE_IN_QUAD, 5000,’y’,x+random.randint(480,550),’rotation-angle-y’,random.randint(180,720)) stage.show() clutter.main()
При условии, что файл Actor (в нашем случае это clutterKoch.py) находится в том же каталоге, это можно запускать и рисовать случайные кривые. Как вы увидите, наши творения можно двигать и вращать. Для этого не нужно заново формировать все точки: на данный момент они являются GL-точками, и об их правильном положении позаботится видеокарта.
Что дальше
Cogls полезен не только при рисовании разных форм. Используя этот интерфейс к OpenGL, можно поменять множество аспектов отображения, вплоть до создания собственного шейдера. На сайте Clutter есть много документации по разным возможностям Cogls. Однако, как мы отметили ранее, она предназначена для программистов на C, и вам придется потратить некоторое время, чтобы это заработало в Python. Взгляните на http://clutter-project.org/docs/cogl/stable.
Мы также небрежно отнеслись к настройке нашего gobject. В сущности, все что мы сделали – это самый минимум, чтобы Actor заработал. Тот, кто правильно обращается с системой, должен зарегистрировать GObject’овские свойства нашего объекта, и можно даже добавить для него собственные сигналы. GObject прекрасен, хотя и сложноват и многословен; увы, здесь мало места, чтобы полностью его раскрыть. Но документация PyGTK содержит много полезной информации о GObject, и если вам интересно, зайдите на http://www.pygtk.org/docs/pygobject.