- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF126:Урок векторной алгебры
Материал из Linuxformat.
- Линейная алгебра для C++
Содержание |
C++ Матрицы и векторы
- Семен Есилевский рассматривает четыре библиотеки, реализующих концепции линейной алгебры, и проводит сравнение их производительности.
 Рис. 1. http://oonumerics.org — портал для вычислительных программистов, работающих с объектно-ориентированными языками.
Рис. 1. http://oonumerics.org — портал для вычислительных программистов, работающих с объектно-ориентированными языками.
Современный прикладной программист, работающий с С++, может годами не вспоминать о том, что компьютеры были изначально созданы для интенсивных математических вычислений. Однако рано или поздно почти каждому разработчику приходится «возвращаться к истокам» и писать вычислительный код, который должен выполняться максимально быстро.
Практически любой вычислительный алгоритм включает множество действий с векторами и матрицами; иными словами, практически все вычислительное программирование базируется на операциях линейной алгебры над одно- или двумерными массивами. Стандартные массивы С++ плохо приспособлены для этих целей:
- Каждый массив – всего лишь указатель, по которому приходится вручную выделять и освобождать память. У матриц это необходимо делать для каждой строки.
- Массивы «не знают» своего размера. Вместе с ними приходится хранить и передавать соответствующие длины.
- Любые действия с массивом как с целым приходиться расписывать поэлементно в виде циклов.
Если используются только векторы (что бывает крайне редко), то на помощь приходит класс valarray из STL. Можно взять и std::vector,но у него гораздо меньше возможностей – в частности, нет перегруженных математических функций для поэлементного доступа. Если же требуется работать с матрицами, то волей-неволей приходится использовать специализированные сторонние библиотеки.
В идеале библиотека линейной алгебры для С++ должна поддерживать запись выражений с векторами и матрицами в естественной математической нотации, иметь удобный интерфейс, поддерживать рутинные операции высокого уровня (такие как решение систем линейных уравнений) и обеспечивать максимальную производительность. Также желательно наличие удобного интерфейса к стандартным библиотекам линейной алгебры BLAS и LAPACK, написанным, как правило, на Fortran (зависит от поставщика) и прекрасно оптимизированным для разных типов процессоров. Производительность этих библиотек считается непревзойденной, но использовать их напрямую в С++ довольно сложно из-за архаичного интерфейса и другого порядка хранения чисел в матрицах.
Цена универсальности
Создание класса, инкапсулирующего векторы и матрицы – любимое упражнение в учебниках по С++, позволяющее продемонстрировать множество полезных приемов. Однако такие «доморощенные» классы неизбежно имеют крайне низкую производительность. Проблема состоит в том, что компилятор С++ не обрабатывает векторы и матрицы в выражениях поэлементно, как это необходимо для оптимальной производительности. В результате в сумме матриц
mat1 = mat2 + mat3;
правая часть сначала будет вычислена и присвоена некоему временному объекту. Затем этот временный объект будет скопирован в mat1 и разрушен. Очевидно, что вызов конструктора и деструктора временного объекта и двукратное копирование данных совершенно излишни, но такова цена универсальности языка С++. Единственный действенный выход из этой ситуации состоит в использовании шаблонов выражений [expression templates]. Эта методика по праву считается одной из самых сложных в программировании на С++, и подробно описывать ее в рамках данной статьи нет смысла. В двух словах можно сказать, что классы, использующие шаблоны выражений, берут на себя часть работы компилятора. Выражения преобразуются путем рекурсивной подстановки шаблонов на этапе компиляции, так что компилятор генерирует оптимальный код без использования ненужных временных переменных. В хорошо спроектированной библиотеке вся эта сложная работа скрыта за простыми интерфейсами классов.
На практике имеет смысл использовать только те библиотеки, которые применяют шаблоны выражений, так как только они имеют производительность, близкую к низкоуровневому коду с явными циклами.
В поисках идеала
Существует множество библиотек линейной алгебры для С++ (внушительный, хотя и неполный, список доступен на портале http://www.oonumerics.org). Даже если отбросить те, которые не используют шаблонов выражений и, следовательно, имеют очень низкую производительность, остается более десяти вариантов. Ниже приведены краткие характеристики четырех наиболее мощных и удобных (с точки зрения автора) библиотек. Для каждой из них представлен фрагмент кода, позволяющий решить систему линейных уравнений и демонстрирующий основные особенности синтаксиса.
uBLAS
Библиотека uBLAS [1] входит в широко используемый набор библиотек Boost, что обеспечивает ей популярность и позволяет надеяться на стандартизацию в будущем. uBLAS поддерживает все основные операции линейной алгебры с плотными и разреженными матрицами разного типа. Имеются функции для решения систем линейных уравнений (впрочем, не очень удобные). Для uBLAS существует хороший интерфейс к LAPACK, но его необходимо устанавливать отдельно, так как он не входит в стандартный набор библиотек Boost. Официальная документация uBLAS откровенно разочаровывает. Она переполнена техническими деталями и не содержит даже простейших примеров рутинных операций.
// Заголовочные файлы входят в общее дерево заголовков boost #include <boost/numeric/ublas/matrix.hpp> #include <boost/numeric/ublas/vector.hpp> // Заголовок для решения систем линейных уравнений силами uBLAS #include <boost/numeric/ublas/lu.hpp> // Интерфейс к LAPACK (нужно устанавливать отдельно) #include <boost/numeric/bindings/traits/ublas_matrix.hpp> #include <boost/numeric/bindings/lapack/gesv.hpp> ... // Пространства имен весьма громоздкие, лучше определить синонимы namespace lapack = boost::numeric::bindings::lapack; namespace ublas = boost::numeric::ublas; // Для совместимости с LAPACK объявляем матрицу упорядоченной по колонкам ublas::matrix<double, ublas::column_major> A(N,N); ublas::vector<double> b(N), x(N); ... // Решаем систему уравнений силами uBLAS // (довольно громоздко и довольно медленно...). ublas::permutation_matrix<std::size_t> pm(A.size1()); // Матрица перестановок ublas::lu_factorize(A, pm); // Факторизуем матрицу ublas::lu_substitute(A, pm,x); // Ищем решение // Решаем систему уравнений силами LAPACK (намного быстрее). //Правая часть должна быть матрицей ublas::matrix<double, ublas::column_major> temp(N,1); column(temp,0) = b; // Доступ к колонкам матрицы реализован процедурами lapack::gesv(A,temp); // Вызов функции LAPACK x = column(temp,0); // Получаем вектор решения // Проверяем точность решения b = prod(A,x); // Произведение матрицы на вектор не записывается в естественной нотации A*x // (как и большинство других операций)
MTL4
Библиотека MTL4 (Matrix Template Library), доступная по адресу [2], как видно из ее названия, изначально построена на шаблонах выражений и имеет очень хорошую производительность в сочетании с естественной математической нотацией. Особое внимание уделено эффективности хранения и обработки разреженных матриц. К сожалению, стремление к технически совершенным способам обработки матриц разного типа выливается в усложнение тривиальных операций. Например, извлечение столбца из матрицы реализовано крайне громоздко и неинтуитивно – с помощью итераторов и курсоров. Документация MTL4 на первый взгляд достаточно подробная и понятная, но при ближайшем рассмотрении оказывается, что многие примеры не компилируются, а использованные в них типы данных и функции попросту не определены.
// Несмотря на путь к заголовочным файлам, MTL4 не входит в boost #include <boost/numeric/mtl/mtl.hpp> // Пространство имен простое и удобное using namespace mtl; //Плотная матрица NxN dense2D<double> A(N,N); // Плотные векторы dense_vector<double> x(N), b(N); … // Линейная система решается предельно интуитивно x = lu_solve(A,b); // Проверяем точность решения b = A*x; // Естественная математическая нотация
Eigen
Eigen [4] является официальной математической библиотекой для среды KDE, но не имеет никаких внешних зависимостей, в том числе и от KDE. Особое внимание здесь уделено элегантности и интуитивности интерфейса. Eigen использует автоматическую параллелизацию многих операций для процессоров, поддерживающих инструкции SSE2. Для часто используемых векторов и матриц размера 2, 3 и 4 используются специальные типы данных, что резко повышает производительность. Сообщения об ошибках в Eigen вполне читабельны, что является большой редкостью для библиотек, использующих шаблоны. Многочисленные внутренние проверки в режиме отладки снижают количество «глупых» ошибок. Документация заслуживает всяческих похвал и содержит в сжатом виде всю информацию, необходимую для применения библиотеки, без лишних технических подробностей.
Из недостатков Eigen можно назвать некоторые нюансы использования, вызванные встроенной параллелизацией, и отсутствие интерфейса к LAPACK. Некоторые функции пока не реализованы, так как библиотека интенсивно развивается.
// Общий заголовок #include <Eigen/Core> // Заголовок для решения систем уравнений #include <Eigen/LU> // Макрос для импорта основных типов данных и функций в текущее пространство имен USING_PART_OF_NAMESPACE_EIGEN; // Динамическая матрица типа double MatrixXd A(N,N); // Динамический вектор типа double VectorXd b(N),x; // Матрица фиксированного размера 3х3 // работает намного быстрее чем MatrixXd s(3); Matrix3d s; // Решаем линейную систему. Нотация полностью объектно-ориентированная. A.lu().solve(b, &x); // Проверяем точность решения // Естественная математическая нотация b = A*x; // Доступ к строкам, столбцам и срезам очень прост b = A.col(k); A.row(k) = x; //Заполнить нулями 10 элементов строки k начиная с третьего A.row(k).segment(3,10).fill(0.0);
GMM++
GMM++ [3] является составной частью мощной и развитой библиотеки Getfem++ для работы с методами конечных элементов (в томчисле для решения систем дифференциальных уравнений). Дизайн GMM++ «навеян» библиотекой MTL ранних версий. Поддерживаются плотные и разреженные матрицы разного типа, которые можно сочетать в выражениях произвольным образом. Имеются все основные стандартные алгоритмы (решение систем линейных уравнений, нахождение собственных значений) и удобный интерфейс для LAPACK и популярной библиотеки для разреженных матриц SuperLU. GMM++ демонстрирует очень хорошую производительность; документация подробная и понятная. К недостаткам GMM++ относятся полное отсутствие естественной математической нотации (интерфейс сугубо процедурный), неунифицированный доступ к элементам векторов и матриц (через operator[] и operator() соответственно), отсутствие специализированных типов для массивов малого размера.
// Интерфейс с LAPACK включается глобальной директивой #define GMM_USES_LAPACK // Основной заголовок #include <gmm/gmm.h> gmm::dense_matrix<double> A(N,N); ©eigen.tuxfamily.org©eigen.tuxfamily.org // В качестве класса для плотных векторов используется std::vector, // и никаких дополнительных «удобств» он не дает std::vector<double> x(N), b(N); // Доступ к элементам матрицы и вектора не унифицирован (операторы () и []) A(2,67) = 1.0; b[5] = 2.0; // b(5), вопреки ожиданиям, не работает ... // Линейная система решается просто gmm::lu_solve(A, x, b); // Все операции записываются в процедурном виде, // естественная нотация не поддерживается mult(A,x,b); // Доступ к срезам матриц довольно громоздкий gmm::sub_matrix(A, gmm::sub_interval(2, 3), gmm::sub_interval(2, 3)); // Доступ к колонкам и строкам матриц прост, но нотация // процедурная, а не объектно-ориентированная gmm::mat_row(A, 5);
Тест производительности
Производительность рассмотренных библиотек оценивалась в четырех тестах, соответствующих разным моделям использования. В первом тесте 10 раз решалась система из 2000 линейных уравнений. Матрица коэффициентов и правая часть заполнялись случайными числами. В случае uBLAS и GMM++ система уравнений решалась как с помощью интерфейса к LAPACK, так и силами самой библиотеки. Во втором тесте 100 раз производилось умножение случайной матрицы размера 2000 × 2000 на соответствующий вектор. Третий тест был аналогичен второму, но использовалась матрица размера 3 × 3 и 1 000 000 умножений. В третьем тесте для uBLAS и Eigen использовались как обычные типы данных, так и специализированные для маленьких массивов фиксированного размера. В четвертом тесте оценивалось время перемножения двух случайных матриц, размер которых варьировался от 10 до 2000.
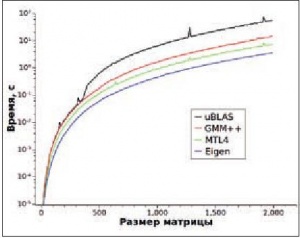
Тест проводился на компьютере с процессором Intel Core 2 Quad Q9300 (тактовая частота 2.5 ГГц) с 32‑битной системой Ubuntu Linux 9.10. Использовался компилятор gcc 4.4.1 с флагами оптимизации ‘-msse2 -O3 -march=native -DNDEBUG’. В случае Eigen использовалась оптимизация -O2, так как более агрессивная оптимизация снижала производительность. Применялась стандартная открытая реализация библиотеки LAPACK версии 3.1, входящая в Ubuntu 9.10. Результаты приведены в таблице и на рис. 2 (время в секундах).
В решении системы уравнений без использования LAPACK лидерами с очень близкими результатами являются GMM++ и uBLAS, а MTL4 и Eigen отстают примерно в полтора раза. Если использовать uBLAS и GMM++ как интерфейсы для LAPACK, то можно добиться более чем двукратного ускорения. В умножении большой матрицы на вектор Eigen, MTL4 и GMM++ демонстрируют одинаковую производительность, а uBLAS отстает почти в 5 раз. При работе с матрицами и векторами размера 3, которые характерны для трехмерной графики, физического моделирования и тому подобных задач, Eigen демонстрирует колоссальное преимущество. Даже при использовании обычных типов данных, не оптимизированных для матриц малого размера, Eigen справляется со своей работой в 12 раз быстрее конкурентов. При использовании специализированных типов данных это преимущество достигает примерно 20000 раз (!). Для сравнения, специальные типы данных в uBLAS улучшают производительность примерно в три раза. Хуже всего справляется с маленькими матрицами MTL4.
При перемножении матриц произвольного размера также с существенным отрывом выигрывает Eigen. Второе место у MTL4. Далее идут GMM++ и uBLAS, которые для небольших матриц демонстрируют одинаковые результаты. Для матриц, больших чем 360 × 360, производительность uBLAS резко падает.
Нужно заметить, что в GMM++ подключение интерфейса к LAPACK происходит «глобально» и оказывает влияние на все операции, в том числе и на те, где дополнительный вызов библиотечной функции «дороже», чем сама операция. В результате при использовании LAPACK резко падает производительность для маленьких матриц.
Для Eigen оптимизация, более агрессивная, чем -O2, снижает производительность. По-видимому, при этом компилятор и внутренние оптимизации библиотеки на уровне шаблонов выражений начинают конфликтовать.
Для uBLAS и GMM++ критичным является использование флага -DNDEBUG, отключающего внутренние проверки и улучшающего производительность на порядок. В Eigen внутренние проверки отключаются автоматически при уровне оптимизации, большем чем -O0.
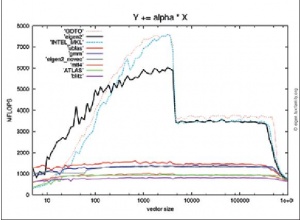
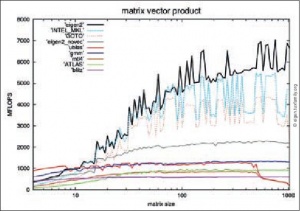
Рассмотренные здесь тесты демонстрируют производительность библиотек в типичных вариантах использования, но, конечно, не являются исчерпывающими. На рисунках приведены некоторые результаты нескольких более строгих сравнительных тестов с официального сайта Eigen.
| Библиотека | Система уравнений | Умножение матрицы 2000 × 2000 на вектор | Умножение матрицы 3 × 3 на вектор |
|---|---|---|---|
| uBLAS | 9.31 | 2.84 | 7.41 (matrix, vector) |
| uBLAS с LAPACK | 3.81 | 2.84 | 2.19 (bounded_matrix, bounded_vector) |
| MTL4 | 14.05 | 0.59 | 21.37 |
| GMM++ | 9.2 | 0.59 | 3.25 |
| GMM++ с LAPACK | 3.85 | 0.6 | 7.92 |
| Eigen | 14.7 | 0.59 | 0.18 (MatrixXd, VectorXd) <0.0001 (Matrix3d, Vector3d) |
Выводы
Из четырех рассмотренных нами библиотек наилучшее впечатление производит Eigen. Она обеспечивает прекрасную производительность (особенно в работе с маленькими матрицами), поддерживает естественную математическую нотацию, имеет простой и интуитивно понятный интерфейс и очень хорошо документирована.
В большинстве случаев Eigen будет оптимальным выбором. Однако поддержка разреженных матриц в Eigen все еще считается экспериментальной, поэтому при интенсивной работе с такими матрицами в качестве альтернативы можно рассматривать MTL4. Функции для решения линейных уравнений, нахождения собственных значений и аналогичные операции в Eigen и MTL4 работают раза в 1,5–2 медленнее, чем соответствующие функции в GMM++ и uBLAS, а использование в последних интерфейса к LAPACK увеличивает этот разрыв еще вдвое.
Если данная разница критична (например, для очень больших матриц) и перевешивает неудобства от неестественного процедурного интерфейса, то разумным выбором могут оказаться uBLAS и GMM++.
За кадром
Из библиотек, не попавших в эту короткую статью, можно назвать следующие:
- Blitz++ (http://www.oonumerics.org/blitz/) – потенциально очень мощная библиотека, однако в ней нет реализации стандартных алгоритмов вроде решения систем линейных уравнений.
- POOMA (http://acts.nersc.gov/pooma/) – библиотека, ориентированная на параллельное решение систем дифференциальных уравнений.
- TNT и JAMA/C++ (http://math.nist.gov/tnt/index.html) – «библиотеки-обертки» над BLAS и LAPACK (наследники LAPACK++).
- SparceLib++ (http://math.nist.gov/sparselib++/) – специализированная библиотека для разреженных матриц.