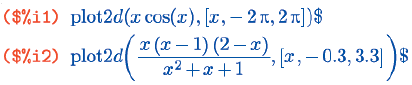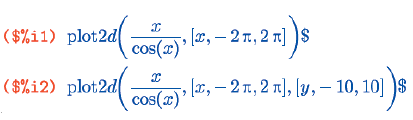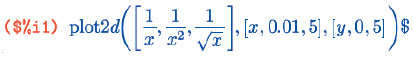- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF85:Maxima
Материал из Linuxformat.
- Учебник Maxima Максимум свободы символьных вычислений
Графики и управляющие конструкции
- ЧАСТЬ 5 Сегодня Тихон Тарнавский продемонстрирует вам «графические» возможности Maxima, а также безупречную работу конструкций if, for и других...
- «А рисовать вы тоже умеете?»
- «Рисовать? Кого-нибудь привлечем.»
Как мы уже говорили в прошлый раз, количество различных функций в Maxima разработчики постарались свести к минимуму, а широту размаха каждой конкретной функции, соответственно, к максимуму. Соблюдается эта тенденция и в функциях построения графиков: основных таких функций всего две, с очевидными, как всегда, названиями – plot2d и plot3d (одно из значений слова «plot» – «график», а аббревиатуры 2d и 3d переводятся как «двумерный» и «трехмерный»). Если говорить точнее, возможности графической отрисовки не встроены в Maxima, а реализованы посредством внешних программ, в чем и прослеживается пресловутый Unix-way: «одна задача – одна программа». По умолчанию, построением графиков занимается gnuplot, но кроме него есть разрабатываемый вместе с Maxima и идущий в ее же пакете openmath. Gnuplot необходимо установить (вручную либо автоматически – как зависимость Maxima) из пакета gnuplot-nox, либо просто gnuplot, а для работы openmath нужен командный интерпретатор wish, входящий обычно в пакет tk; и, начиная с версии 5.10.0, еще и xMaxima.
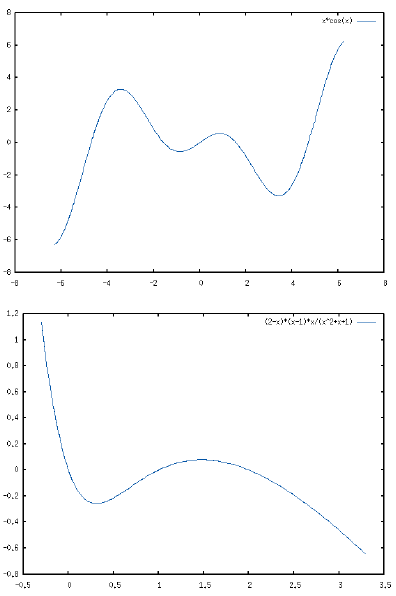
Теперь кратко – о возможностях. Начнем с plot2d. Кратчайший вариант ее вызова такой: plot2d(выражение, [символ, начало, конец]), где выражение задает функцию, график которой нужно построить, символ – неизвестное (он, понятное дело, должен быть единственным неопределенным символом, входящим в выражение), а начало и конец задают отрезок оси Х для построения графика; участок по оси Y в таком варианте записи выбирается автоматически, исходя из минимума и максимума функции на заданном промежутке. Обратите внимание, что неизвестное и концы промежутка нужно задавать не тремя отдельными параметрами, как, скажем, в integrate, а в виде списка. Это связано с тем, что plot2d может принимать еще и дополнительные аргументы – в таком случае они перечисляются следом за таким списком, что исключает всякую путаницу.
После вызова функции plot2d в таком варианте откроется окно gnuplot, в котором будет отображен затребованный график. Никакой интерактивной работы с полученным изображением gnuplot не предусматривает, кроме автоматического его масштабирования при изменении размеров окна. Насмотревшись вдоволь, можно закрыть окно с графиком клавишей Q, либо, в случае работы с Maxima в редакторе TeXmacs или wxMaxima, просто переключиться обратно в интерфейс, оставив окно gnuplot открытым, и продолжить работу:
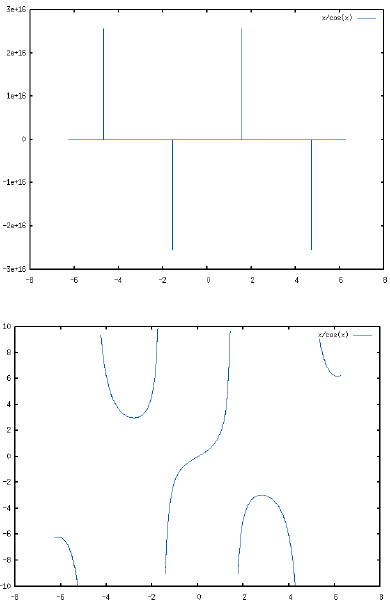
В некоторых случаях автоматический подбор отображаемого участка вертикальной оси может нас не устроить. Например, он работает не очень хорошо, если функция имеет на заданном промежутке точку разрыва, хотя бы один из односторонних пределов в которой равен бесконечности: тогда промежуток по оси Y будет выбран слишком большим. Да и в других случаях может понадобиться изменить умолчательное поведение. Для этого предусмотрен такой вариант вызова функции: plot2d(выражение, [символ, начало, конец], [y, начало, конец]). Здесь буква y используется в качестве обозначения вертикальной оси, а остальные два параметра имеют тот же смысл, что и выше.
Как видите, умолчательный вид графиков в gnuplot достаточно прост и даже аскетичен, но здесь можно очень и очень многое менять с помощью дополнительных опций. Некоторые из которых будут освещены чуть ниже, а остальные можно изучить по документации к gnuplot.
Чтобы построить на одной и той же картинке одновременно два графика (или больше), просто передайте функции plot2d вместо отдельного выражения их список:
Здесь [x, 0.01, 5] вместо [x, 0, 5] я написал «по привычке» – Maxima 5.9.x выдавала ошибку, если заданная функция была не определена на одном из концов интервала. В 5.10.0 мне эту ошибку воспроизвести не удалось; так что есть основания полагать, что поведение в таких случаях поправили.
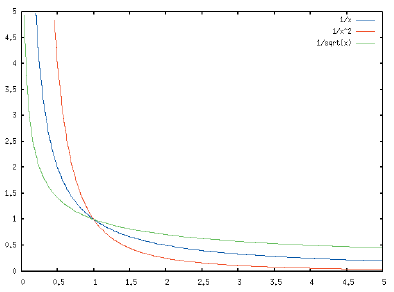
Может plot2d строить и графики параметрически заданных функций. Для этого используется список с ключевым словом parametric: plot2d([parametric, x-выражение, y-выражение, [переменная, начало,конец], [nticks, количество]]). Здесь «x-выражение» и «y-выражение» задают зависимость координат от параметра, то есть, по сути, это две функции вида x(t), y(t), где t – переменная параметризации. Эта же переменная должна фигурировать в следующем аргументе-списке, а параметры «начало», «конец», как и в двух других рассмотренных случаях, задают отрезок, в пределах которого этот параметр будет изменяться. Последний аргумент-список, с ключевым словом nticks, задает количество кусочков, на которые будет разбит интервал изменения параметра при построении графика. Этот аргумент опционален, но на практике он нужен почти всегда: умолчательное значение nticks равно 10; согласитесь, редко бывает нужно в качестве графика получить ломаную из 10 отрезков. Вот пример построения графика параметрической функции:
Кроме parametric, функция plot2d понимает еще одно ключевое слово: discrete. Предназначено оно, как нетрудно догадаться, для отображения на плоскости дискретных множеств; точнее говоря, конечных наборов точек. По записи аргументов такой вариант распадается еще на два: plot2d([discrete, x-список, y-список]) и plot2d([discrete, [x, y]-список]). В первом варианте координаты задаются как два отдельных списка [x1, x2, ..., xn], [y1, y2, ..., yn], а во втором – как список пар координат отдельных точек [[x1, y1], [x2, y2], ..., [xn, yn]].
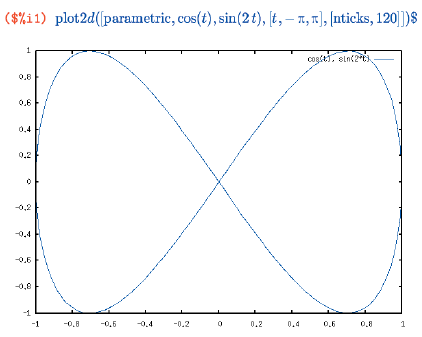
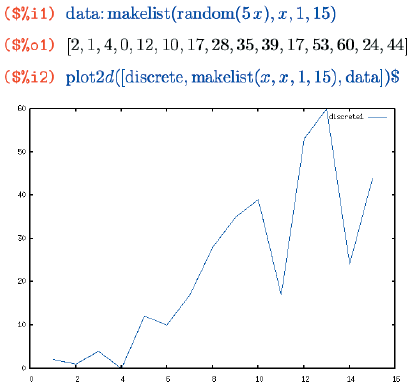
Если мы, к примеру, имеем набор статистических значений, зависящих от номера, мы можем отобразить его, задав в качестве x-координат сами эти номера, то есть натуральные числа:
По умолчанию множество отображается в виде ломаной с вершинами в заданных точках; такое поведение можно изменить и получить вывод, к примеру, в виде отдельных точек. Это достигается использованием специальных опций, применимых как к plot2d, так и к plot3d, поэтому давайте перейдем к рассмотрению последней.
Придаем объем
Функция plot3d имеет два варианта вызова: один для явного задания функции и один для параметрического. В обоих случаях функция принимает три аргумента. Для явно заданной функции: plot3d(выражение,[переменная1, начало, конец], [переменная2, начало, конец]); аргументы аналогичны plot2d, с той разницей, что здесь независимых переменных две.