- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF85:LaTeX
Материал из Linuxformat.
Версия 23:04, 10 марта 2008
Содержание |
Компьютерные Teхнологии: Учимся использовать культовую систему вёрстки LaTeX
Набор математики: снова в школу
ЧАСТЬ 3: Успешно пройдя две ступени посвящения, вы готовы двинуться в путь к вершинам мастерства. Вашим проводником в этом нелегком деле будет Евгений Балдин.
Полиграфисты относят математические работы к каторжным… Д.Э. Кнут. Математическая типография.
Иногда от незнакомых с TeXнологиями людей приходится слышать, что LaTeX годится только для набора математики. При знакомстве же с истинными TeXнологиями возникает понимание, что LaTeX настолько хорош, что с его помощью можно набирать даже математику.
Набор математических формул всегда считался вершиной типографского искусства. Дело в том, что формулы, для концентрации информации и дополнительной выразительности по сравнению с обычным текстом, являются многоуровневыми. Д.Э. Кнут к своей программе компьютерной типографии создал и язык для описания формул. После короткого периода обучения пользователь в состоянии читать и набирать на этом языке формулы практически любой сложности.
LaTeX – не единственная программная среда, использующая TeXнотацию. Эта же нотация рекомендуется при наборе всех скольконибудь сложных формул на страницах Википедии (http://ru.wikipedia.org статья «Википедия:Формулы»).Становлению TeX как стандарта для набора формул в значительной степени поспособствовало Американское математическое сообщество (The American Mathematical Society – AMS), которое субсидировало разработку расширения TeX, известного как AMSTeX, в начале восьмидесятых годов прошлого столетия. В 1987 году наработки AMSTeX были добавлены в LaTeX в виде пакета amsmath. Вместе с amsmath в LaTeX было добавлено множество улучшений, позволяющих набирать действительно изощрённую математику. Поэтому при использовании в тексте математики в шапке документа следует в обязательном порядке загружать пакет amsmath:
\usepackage{amsmath}
В дальнейшем предполагается, что этот пакет уже загружен.Полностью описать все команды языка для набора формул в рамках короткой статьи нереально, так как математика, как и способы её представления, безгранична. Поэтому основное внимание будет уделено базовым правилам и русскому стилю в формулах. В любой сколько-нибудь большой книге по LaTeX будет полный список всех команд. Если серьёзно работать с математикой, то подобная книжка, в любом случае, понадобится.
Набор формул
При формировании текста формулы подразделяются на строчные и выносные. Строчные формулы набираются внутри абзаца вместе текстом. По описанию формулы LaTeX создаёт бокс, который обрабатывается наравне с обычными текстовыми боксами. Как правило, строковые формулы это небольшие вставки, вроде E=mc2. Выносные или выключенные формулы выводятся за пределы абзаца.
Строчная формула в тексте ограничивается[1] с помощью символа доллара $«формула»$ или с помощью команд-скобок \(«формула»\). При наборе предпочтительнее использовать второй вариант оформления, так как он позволяет легко определить, где начинается, а где кончается формула. «Долларовое» ($) окружение лучше тем, что оно чуть-чуть короче, кроме этого, команда $ крепкая[2], в отличие от команд-скобок.
Однострочные выносные формулы формируются с помощью окружения equation. Так как в этом случае формула вынесена за пределы абзаца, то её можно пронумеровать. Например:
\begin{equation}
\label{eq:math:ex1}
\int\limits_{-\infty}^{\infty}
e^{-x^2/2}dx=\sqrt{2\pi}
\end{equation}
| Невозможно разобрать выражение (неизвестная ошибка\begin): \begin{equation}\label{eq:math:ex1}\int\limits_{-\infty}^{\infty}e^{-x^2/2}dx=\sqrt{2\pi}\end{equation} |
Нумерация формул удобна для того, чтобы позже в тексте на неё можно было легко сослаться с помощью команды \eqref{eq:math:1}[3]. Если же формул немного и не хочется никакой нумерации, то можно воспользоваться окружением equation*[4]. При создании выключенной формулы размер шрифта для улучшения читаемости немного увеличивается. LaTeX имеет несколько стилей для оформления математических формул. При желании можно выбрать необходимый стиль вручную:
- \displaystyle – стиль, используемый для выносных формул,
- \textstyle – стиль строчных формул,
- \scriptstyle – в этом стиле набираются индексы,
- \scriptscriptstyle – индексы второго уровня.
С помощью этих команд можно увеличить размер шрифта для формул внутри абзаца, или заставить индексы выглядеть как базовые символы. Например, сравните:
\begin{equation*}
\frac{1}{1+
\frac{1}{1+
\frac{1}{1+
\frac{1}{2}}}}
\end{equation*}
| Невозможно разобрать выражение (неизвестная ошибка\begin): \begin{equation*}\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{2}}}}\end{equation*} |
и
\begin{equation*}
\frac{1}{\displaystyle 1+
\frac{1}{\displaystyle 1+
\frac{1}{\displaystyle 1+
\frac{\displaystyle 1}
{\displaystyle 2}}}}
\end{equation*}
| Невозможно разобрать выражение (неизвестная ошибка\begin): \begin{equation*}\frac{1}{\displaystyle 1+\frac{1}{\displaystyle 1+\frac{1}{\displaystyle 1+\frac{\displaystyle 1}{\displaystyle 2}}}}\end{equation*} |
Пробелы в формулах отмечают только конец команды, а сами по себе смысла не имеют – LaTeX, как правило, гораздо лучше знает, как сформировать результат.
Кириллица в формулах
Всё дело в имеющихся шрифтах – они красивые, разнообразные, но в большинстве своём англоязычные. В настоящее время кириллические математические шрифты в «дикой природе» отсутствуют, поэтому приходится пользоваться их текстовыми версиями.
Стиль mathtext (пакет t2), позволяет использовать кириллицу в формулах без дополнительных ухищрений. Стиль может быть подключён с опцией warn – в этом случае он сообщает обо всех случаях использования кириллических букв в формулах. mathtext следует загружать до babel и/или fontenc.
\usepackage[warn]{mathtext}
\[
v_{ср}=\frac{S_{конец}-S_{начало}}
{\delta t}
\]
| Невозможно разобрать выражение (неизвестная ошибка): \[v_{ср}=\frac{S_{конец}-S_{начало}}{\delta t}\] |
Здесь для создания выключенной формулы используется команда \[«формула»\] – краткий аналог окружения equation*. В отличие от латиницы, русские буквы в формулах печатаются прямым шрифтом – это было сделано специально. Чтобы изменить это поведение, в преамбуле следует добавить команду для переопределения шрифта:
\DeсlareSуmbolFont{T2Aletters}{T2A}{cmr}{m}{it}
Стиль amstext (загружается автоматически при загрузке amsmath) определяет команду \text, которая позволяет вставлять в формулу обычный текст. Он может быть и русским:
\[v_{ср}=
\frac{\text{конец пути}-
\text{начало пути}}
{\text{время в пути}}\]
| Невозможно разобрать выражение (неизвестная ошибка): \[v_{ср}=\frac{\text{конец пути}-\text{начало пути}}{\text{время в пути}}\] |
Преимущество такого подхода заключается в том, что внутри команды \text пробелы воспринимаются как нормальные символы и слова не сливаются. Использование \text предпочтительно и для целей переносимости.
Школьная математика
Математика в школе – это явление, через которое проходит каждый. Именно поэтому фактически любой вменяемый россиянин умеет обращаться с дробями, знает теорему Пифагора, с лёгкостью решает квадратные уравнения и что-то слышал про интеграл и производную. Разберёмся со всем этим поподробнее.
Индексы
Букв в латинском алфавите не так уж и много, а научных понятий – без числа. Один из способов отличать обозначения друг от друга – это индексы, как верхние, так и нижние:
|
\[A_{\text{нижний индекс}}\quad B^{\text{верхний индекс}}\quad C_n^k\] | Невозможно разобрать выражение (неизвестная ошибка): \[A_{\text{нижний индекс}}\quadB^{\text{верхний индекс}}\quadC_n^k\] |
Обратите внимание, что если в индексе ровно один знак, то фигур- ные скобки вокруг него можно и нужно опустить. Теперь мы можем записать теорему Пифагора: \(a^2+b^2=c^2\) a2 + b2 = c2
Математические символы
Кроме символов латиницы и кириллицы, математики используют множество самых разнообразных значков, да и латиница не так уж проста. Если воспользоваться пакетом amsfonts, то она может стать такой:
\begin{itemize}
\item \(ABCD\) "--- обычной,
\item \(\mathbf{ABCD}\) "--- жирной,
\item \(\mathbb{ABCD}\) "--- ажурной,
\item \(\mathcal{ABCD}\) "---прописной.
\end{itemize}
| Невозможно разобрать выражение (неизвестная ошибка\begin): \begin{itemize}\item \(ABCD\)\item \(\mathbf{ABCD}\)\item \(\mathbb{ABCD}\)\item \(\mathcal{ABCD}\)\end{itemize} |
Это далеко не все возможные шрифтовые стили которые можно применять в математической моде, но лучше особо не перегружать формулы всякой «готикой» (например, \mathfrak). Не единой латиницей жив математик. Традиционно, везде, где только можно, используются греческие буквы.
| Буква | Команда | Буква | Команда | Буква | Команда |
|---|---|---|---|---|---|
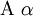 | \Alpha \alpha | 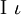 | \Iota \iota | 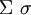 | \Sigma \sigma |
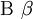 | \Beta \beta | 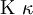 | \Kappa \kappa | 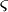 | \varsigma |
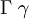 | \Gamma \gamma | 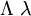 | \Lambda \lambda | 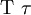 | \Tau \tau |
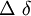 | \Delta \delta | 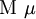 | \Mu \mu | 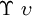 | \Upsilon \upsilon |
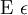 | \Epsilon \epsilon | 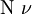 | \Nu \nu | 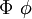 | \Phi \phi |
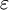 | \varepsilon | 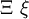 | \Xi \xi | 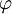 | \varphi |
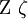 | \Zeta \zeta | 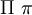 | \Pi \pi | 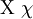 | \Chi \chi |
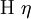 | \Eta \eta | 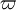 | \varpi | 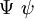 | \Psi \psi |
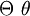 | \Theta \theta | 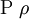 | \Rho \rho | 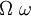 | \Omega \omega |
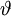 | \vartheta | 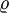 | \varrho |
В LaTeX присутствует полный набор и, за исключением трёх букв, начертание вполне привычное. Для исправления непривычных начертаний эти буквы были переопределены с помощью пакета amssymb:
%Переопределение kappa epsilon phi на русский лад
\renewcommand{\kappa}{\varkappa}
\renewcommand{\epsilon}{\varepsilon}
\renewcommand{\phi}{\varphi}
Спецсимволов в LaTeX великое множество. В стандартной поставке TeX Live идёт «Всеобъемлющий список сиволов LaTeX» (The Comprehensive LaTeX Symbols List – файл symbols-a4.pdf) в котором перечислено 3300 распространённых символов, применяемых пользователями LaTeX. Почти наверняка любой операнд, который вам нужен, там уже есть. Ниже будет перечислена только та часть символов, которая, с моей точки зрения, может пригодиться в наборе школьной математики. Пакет amssymb для использования обязателен.
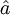 | \hat{a} | 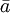 | \bar{a} | 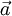 | \vec{a} | 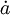 | \dot{a} | 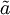 | \tilde{a} |
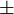 | \pm | 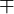 | \mp | 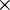 | \times |  | \cdot | 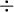 | \div |
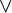 | \lor | 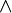 | \land |  | \neg | 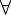 | \forall | 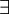 | \exists |
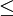 | \le | 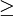 | \ge | 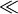 | \ll | 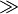 | \gg | 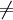 | \neq |
 | \equiv | ˜ | \sim | 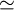 | \simeq | 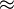 | \approx | 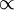 | \propto |
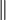 | \parallel | 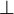 | \perp | 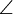 | \angle |  | \triangle | 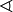 | \sphericalangle |
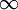 | \infty | 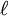 | \ell | 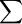 | \sum | 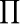 | \prod | 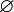 | \varnothing |
Для соответствия русским традициям 2 символа были переопределены:
%Переопределение le ge на русский лад
\renewcommand{\le}{\leqslant}
\renewcommand{\ge}{\geqslant}
Дроби
Дроби формируются с помощью команды \frac[5]:
\[
дробь=\frac{числитель}{знаменатель}
\]
| 
|
Как и практически вся математика в LaTeX, дробь записывается так, как читается само выражение.
Корни
Для рисования знака корня используется команда
\sqrt[степень]{«подкоренное выражение»}
Степень можно упустить. В этом случае рисуется обычный квадратный корень.
|
\[ \overline{ \underline{\Large \sqrt[3]{a}+\sqrt[2]{b}+\sqrt[99]{g} } } \] | Невозможно разобрать выражение (неизвестная ошибка\Large): \overline{\underline{\Large\sqrt[3]{a}+\sqrt[2]{b}+\sqrt[99]{g}}} |
Обратите внимание, что знак корня размещается в соответствии с размерами подкоренного выражения. Если в выражении присутствует только один корень, то это самое разумное поведение, но в случае нескольких корней, как в приведённом выше примере, не помешает выравнивание.
Для выравнивания по высоте используется команда \mathstrut[6]. В результате её применения вставляется невидимый символ нулевой толщины и высоты, в точности равной высоте круглой скобки:
\[\Large
\sqrt[3]{\mathstrut a}+
\sqrt[2]{\mathstrut b}+
\sqrt[99]{\mathstrut g}
\]
| Невозможно разобрать выражение (неизвестная ошибка): \[\Large\sqrt[3]{\mathstrut a}+\sqrt[2]{\mathstrut b}+\sqrt[99]{\mathstrut g}\] |
Квадратное уравнение
И, наконец, вершина школьной математики – это решение квадратного уравнения ax2+bx+c=0:
\[
x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}
\]
| 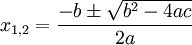
|
Теперь можно смело садиться за написание методичек.
Функции
Все символы в математической моде печатаются курсивом, поэтому названия функций, для выделения, печатаются прямым шрифтом. Кроме смены шрифта, функции с обоих сторон должны правильно «отбиваться» пробелами, иначе будет некрасиво. При загрузке русского языка с помощью пакета babel кроме стандартных имён функций доопределяется несколько сокращений, применяемых в русскоязычной литературе. Среди часто употребляемых функций можно упомянуть: cos, arccos, sin, arcsin, tg, arctg, ctg, arcctg, sh, ch, th, cth, exp, ln, log, lim, min и max. В математической моде эти функции можно использовать в качестве команд:
\begin{equation*}
\begin{split}
&\log_2 10=\ln10/\ln2\simeq3.32 \\
&\lim_{x\to0}\frac{\sin x}{x}=1\\
&(a+b)^n=\sum_{k=1}^n C^k_n a^kb^{n-k}
\end{split}
\end{equation*} | Невозможно разобрать выражение (неизвестная ошибка\begin): \begin{equation*}\begin{split}&\log_2 10=\ln10/\ln2\simeq3.32 \\&\lim_{x\to0}\frac{\sin x}{x}=1\\&(a+b)^n=\sum_{k=1}^n C^k_n a^kb^{n-k}\end{split}\end{equation*} |
Обратите внимание на обработку индексов для функции log (логарифм) и lim (предел). Для доопределения новых функций правильнее всего воспользоваться в преамбуле командой DeclareMathOperator: %В преамбуле - определение новых функций \DeclareMathOperator{\log-like}{log-like} \DeclareMathOperator*{\lim-like}{lim-like} В зависимости от варианта команды индексы отображаются как для логарифма (команда без звёздочки) или как для предела (команда со звёздочкой). Производная и интеграл В старших классах, в конце обучения, обычно чуть-чуть касаются поня- тий интегрирования и дифференцирования. Возможно, для того, чтобы правильно подсчитать сдачу в магазине, эти знания не являются необ- ходимыми. Но для изучения физики и, как следствие, химии и биоло- гии без интегралов никак – поверьте мне на слово. Производная обычно отмечается штрихом. В физике, производная по времени выделяется точкой, для того чтобы отличать её от произ- водной по координате. Можно честно написать \frac{d F(x)}{dx}. Для час- тной производной вместо буквы d используется спецсимвол \partial:
to be continued…
Примечания
- ↑ Есть более формальное оформление строчной формулы как окружения: \begin{math} «формула» \end{math}. Но, в силу понятных причин, никто подобное описание не использует.
- ↑ Начав изучать команды LaTeX, довольно быстро сталкиваешься с понятиями «хрупкости»/«крепкости». «Крепкие» команды, в отличие от «хрупких», можно использовать в качестве аргументов других команд. С другой стороны, хрупкие команды тоже можно использовать как параметры, защитив их с помощью команды \protect. Эти понятия в большинстве своём пережитки прошлого и их постепенно изживают, но пока следует иметь их в виду.
- ↑ Метка выставляется с помощью команды \label.
- ↑ К equation добавляется звёздочка. Подобный приём в создании команд применяется достаточно часто. Команда со * обычно не нумеруется и не отображается ни в каких автоматически составляемых списках.
- ↑ От слова fraction – «дробь».
- ↑ От английского strut – «подпорка» или «страта».


