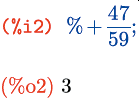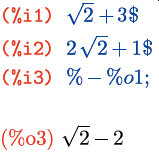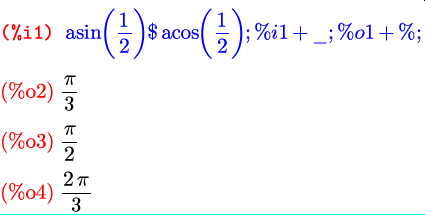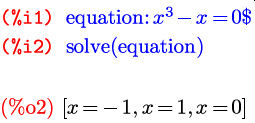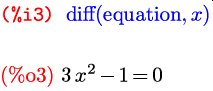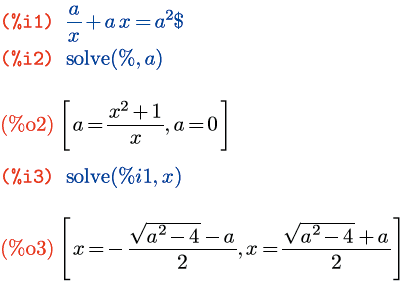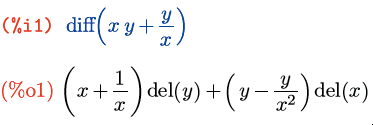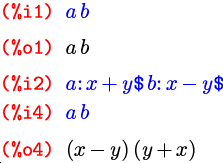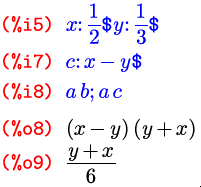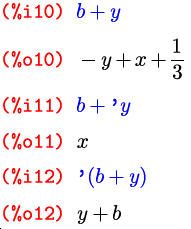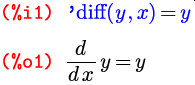- Подписка на печатную версию:
- Подписка на электронную версию:
- Подшивки старых номеров журнала (печатные версии)
LXF81:Maxima
Материал из Linuxformat.
(Новая: ==Maxima – максимум свободы символьных вычислений== ''часть 1 На носу вступительные экзамены? Спрятанный п...) |
|||
| Строка 51: | Строка 51: | ||
представляют два интерфейса. | представляют два интерфейса. | ||
| + | [[Изображение:Img_81_93_4.png|200px|left|thumb|Рисунок 1. wxMaxima.]] | ||
Первый – это отдельная самостоятельная графическая программа по | Первый – это отдельная самостоятельная графическая программа по | ||
имени wxMaxima (рис. 1). Она, как и сама Maxima, помимо Linux/*BSD | имени wxMaxima (рис. 1). Она, как и сама Maxima, помимо Linux/*BSD | ||
| Строка 66: | Строка 67: | ||
вводить все команды с клавиатуры. Кроме того, wxMaxima предоставляет удобный интерфейс к документации по системе; хотя, так как документация поставляется в формате html, вместо этого можно использовать обычный браузер. | вводить все команды с клавиатуры. Кроме того, wxMaxima предоставляет удобный интерфейс к документации по системе; хотя, так как документация поставляется в формате html, вместо этого можно использовать обычный браузер. | ||
| + | [[Изображение:Img_81_93_5.png|200px|right|thumb|Рисунок 2.Maxima-сессия в редакторе TeXmacs.]] | ||
Второй достаточно интересный интерфейс к Maxima – это дополнительный режим в редакторе TeXmacs. Хотя этот редактор имеет общее | Второй достаточно интересный интерфейс к Maxima – это дополнительный режим в редакторе TeXmacs. Хотя этот редактор имеет общее | ||
историческое прошлое с широко известным Emacs, что явствует из | историческое прошлое с широко известным Emacs, что явствует из | ||
| Строка 120: | Строка 122: | ||
простейшем случае, точкой с запятой. После ввода команды и нажатия | простейшем случае, точкой с запятой. После ввода команды и нажатия | ||
«Enter» Maxima выведет результат и будет ожидать следующей команды: | «Enter» Maxima выведет результат и будет ожидать следующей команды: | ||
| + | [[Изображение:Img_81_93_1.png|center]] | ||
Для арифметических действий используются традиционные обозначения: –, +, *, /; ** или ^ для возведения в степень, sqrt() для квадратного корня. | Для арифметических действий используются традиционные обозначения: –, +, *, /; ** или ^ для возведения в степень, sqrt() для квадратного корня. | ||
| Строка 126: | Строка 129: | ||
врезке математическим режимом ввода редактора TeXmacs. К примеру, | врезке математическим режимом ввода редактора TeXmacs. К примеру, | ||
приведенный выше код выглядел бы так: | приведенный выше код выглядел бы так: | ||
| + | [[Изображение:Img_81_93_2.png|center]] | ||
Если для каких-то обозначений будет неочевидно, как записать их в | Если для каких-то обозначений будет неочевидно, как записать их в | ||
| Строка 142: | Строка 146: | ||
по ее имени, подставляя его в любые выражения. Кроме того последняя ячейка вывода обозначается через %, а последняя ячейка ввода – через _. Это позволяет обращаться к последнему результату, не | по ее имени, подставляя его в любые выражения. Кроме того последняя ячейка вывода обозначается через %, а последняя ячейка ввода – через _. Это позволяет обращаться к последнему результату, не | ||
отвлекаясь на то, каков его номер. | отвлекаясь на то, каков его номер. | ||
| + | [[Изображение:Img_81_93_3.png|center]] | ||
Здесь %+47/59 – то же самое, что %o1+47/59. | Здесь %+47/59 – то же самое, что %o1+47/59. | ||
| Строка 148: | Строка 153: | ||
результат при этом все равно вычисляется; как видите, в этом примере | результат при этом все равно вычисляется; как видите, в этом примере | ||
ячейки %o1 и %o2 доступны, хотя и не показаны (к ячейке %o2 обращение идет через символ %, смысл которого расшифрован выше): | ячейки %o1 и %o2 доступны, хотя и не показаны (к ячейке %o2 обращение идет через символ %, смысл которого расшифрован выше): | ||
| + | [[Изображение:Img_81_94_2.png|center]] | ||
Каждую следующую команду не обязательно писать с новой | Каждую следующую команду не обязательно писать с новой | ||
| Строка 154: | Строка 160: | ||
строке после метки %i1 введены ячейки от %i1 до %i4; в ячейке %i3 | строке после метки %i1 введены ячейки от %i1 до %i4; в ячейке %i3 | ||
используются %i1 и %i2 (обозначенная как _ – предыдущий ввод): | используются %i1 и %i2 (обозначенная как _ – предыдущий ввод): | ||
| + | [[Изображение:Img_81_94_3.png|center]] | ||
В wxMaxima и TeXmacs последнюю или единственную команду в | В wxMaxima и TeXmacs последнюю или единственную команду в | ||
| Строка 168: | Строка 175: | ||
Максимы – символьная запись и аналитические вычисления, уравнения | Максимы – символьная запись и аналитические вычисления, уравнения | ||
достаточно часто используются. Например: | достаточно часто используются. Например: | ||
| + | [[Изображение:Img_81_94_4.png|center]] | ||
В каком-то смысле двоеточие даже нагляднее в таком контексте, чем | В каком-то смысле двоеточие даже нагляднее в таком контексте, чем | ||
знак равенства: это можно понимать так, что мы задаем некое обозначение, а затем через двоеточие расшифровываем, что именно оно обозначает. После того, как выражение поименовано, мы в любой момент можем | знак равенства: это можно понимать так, что мы задаем некое обозначение, а затем через двоеточие расшифровываем, что именно оно обозначает. После того, как выражение поименовано, мы в любой момент можем | ||
вызвать его по имени: | вызвать его по имени: | ||
| + | [[Изображение:Img_81_94_5.png|center]] | ||
Любое имя можно очистить от присвоенного ему выражения функцией kill(), и освободить занимаемую этим выражением память. Для | Любое имя можно очистить от присвоенного ему выражения функцией kill(), и освободить занимаемую этим выражением память. Для | ||
| Строка 189: | Строка 198: | ||
Например, функция solve, которую мы использовали с одним аргументом, чаще вызывается с двумя аргументами. Первый задает уравнение | Например, функция solve, которую мы использовали с одним аргументом, чаще вызывается с двумя аргументами. Первый задает уравнение | ||
или функцию, чьи корни надо найти; второй – переменную, относительно которой нужно решать уравнение: | или функцию, чьи корни надо найти; второй – переменную, относительно которой нужно решать уравнение: | ||
| + | [[Изображение:Img_81_95_1.png|center]] | ||
Если формула, задающая решаемое уравнение, содержит только | Если формула, задающая решаемое уравнение, содержит только | ||
| Строка 196: | Строка 206: | ||
Вторая функция из наших новых знакомых – diff – также может принимать один аргумент; в этом случае она находит дифференциал заданного выражения: | Вторая функция из наших новых знакомых – diff – также может принимать один аргумент; в этом случае она находит дифференциал заданного выражения: | ||
| + | [[Изображение:Img_81_95_2.png|center]] | ||
Через del(x) и del(y) здесь обозначены дифференциалы соответствующих символов. | Через del(x) и del(y) здесь обозначены дифференциалы соответствующих символов. | ||
| Строка 210: | Строка 221: | ||
текст, после чего предлагают ввести номер того раздела или описания той | текст, после чего предлагают ввести номер того раздела или описания той | ||
функции, которые вы хотите посмотреть: | функции, которые вы хотите посмотреть: | ||
| + | [[Изображение:Img_81_95_3.png|center]] | ||
Когда вы выберете раздел, будет выдано его содержимое: | Когда вы выберете раздел, будет выдано его содержимое: | ||
| + | [[Изображение:Img_81_96_1.png|center]] | ||
Если для слова, которое вы ввели после ? или describe, найдено | Если для слова, которое вы ввели после ? или describe, найдено | ||
| Строка 219: | Строка 232: | ||
использования. Пример можно загрузить функцией example(). Вызов | использования. Пример можно загрузить функцией example(). Вызов | ||
этой функции без аргумента отобразит список всех имен доступных примеров; вызов вида example(name) загрузит в текущую сессию и выполнит указанный файл примера: | этой функции без аргумента отобразит список всех имен доступных примеров; вызов вида example(name) загрузит в текущую сессию и выполнит указанный файл примера: | ||
| + | [[Изображение:Img_81_96_2.png|center]] | ||
| + | |||
===Основные принципы=== | ===Основные принципы=== | ||
{{Врезка | {{Врезка | ||
| Строка 237: | Строка 252: | ||
ни с чем, будет представлять самого себя, трактуемого опять-таки как | ни с чем, будет представлять самого себя, трактуемого опять-таки как | ||
выражение. Поясним на примере: | выражение. Поясним на примере: | ||
| + | [[Изображение:Img_81_96_3.png|center]] | ||
Из этого следует, в частности, что в выражение автоматически подставляется значение входящего в него символа только в том случае, если | Из этого следует, в частности, что в выражение автоматически подставляется значение входящего в него символа только в том случае, если | ||
это значение было приписано символу до определения выражения: | это значение было приписано символу до определения выражения: | ||
| + | [[Изображение:Img_81_96_4.png|center]] | ||
Если некоторый символ уже имеет какое-то значение, можем ли мы | Если некоторый символ уже имеет какое-то значение, можем ли мы | ||
| Строка 245: | Строка 262: | ||
Сделать это можно с помощью знака апострофа – введенный перед | Сделать это можно с помощью знака апострофа – введенный перед | ||
любым символом или выражением, он предотвращает его вычисление: | любым символом или выражением, он предотвращает его вычисление: | ||
| + | [[Изображение:Img_81_96_5.png|center]] | ||
Результат выражения %i12 был бы аналогичен и в том случае, если | Результат выражения %i12 был бы аналогичен и в том случае, если | ||
| Строка 255: | Строка 273: | ||
пригодиться нам для обозначения производной в дифференциальном | пригодиться нам для обозначения производной в дифференциальном | ||
уравнении; в этом случае, конечно, вычислять ее не надо: | уравнении; в этом случае, конечно, вычислять ее не надо: | ||
| + | [[Изображение:Img_81_96_6.png|center]] | ||
Благодаря описанным особенностям работа в Максиме, с одной | Благодаря описанным особенностям работа в Максиме, с одной | ||
Версия 15:42, 14 марта 2008
Содержание |
Maxima – максимум свободы символьных вычислений
часть 1 На носу вступительные экзамены? Спрятанный под партой КПК с Linux может оказаться куда полезнее самой изощренной шпаргалки! Впрочем, он может сослужить добрую службу и принимающей стороне, а также всем, кому приходится много считать. Как? Спросите у Тихона Тарнавского!
Максима в науке и образовании
Среди математического ПО для аналитических (символьных) вычислений наиболее широко известно коммерческое (Maple, Mathematica); это очень мощный инструмент для ученого или преподавателя, аспиранта или студента, позволяющий автоматизировать наиболее рутинную и требующую повышенного внимания часть работы, оперирующий при этом аналитической записью данных, т.е. фактически математическими формулами. Такую программу можно назвать средой программирования, с той разницей, что в качестве элементов языка программирования выступают привычные человеку математические обозначения.
Программа, которая стала темой статьи, работает на тех же принципах и предоставляет похожий функционал; самое радикальное ее отличие – то, что она не является ни коммерческой, ни закрытой. Другими словами, речь идет о свободной программе. На самом деле использование свободного ПО более естественно для фундаментальной науки, нежели коммерческого, так как модель, которая используется в свободном ПО – это модель открытости и общедоступности всех наработок. Очевидно, эти же свойства присущи и результатам научной деятельности. Используя такую схожесть подходов, можно фактически рассматривать расширения функционала свободных программ или дополнительные библиотеки, которые могут создаваться для своих нужд в процессе научных исследований, как неотъемлемую часть результатов таких исследований. И эти результаты могут использоваться и распространяться на усмотрение пользователя без оглядки на ограничения, налагаемые лицензиями исходного ПО. В случае же коммерческого ПО, которое находится в собственности его производителя, такого рода свободы значительно ограничены, начиная от невозможности свободно (и законно) передавать само такое ПО вместе с наработками и вплоть до возможных патентных исков от компании-разработчика ПО в случае распространения самодельных дополнительных библиотек к нему.
С другой стороны, основное направление, кроме научных разработок, где такие программы востребованы – это высшее образование; а использование для учебных нужд именно свободного ПО – это реальная возможность и для вуза, и для студентов и преподавателей иметь в своем распоряжении легальные копии такого ПО без больших, и даже сколь-нибудь существенных, денежных затрат.
Эта статья открывает цикл, посвященный свободной программе аналитических вычислений Maxima. Этим циклом я постараюсь дать вам наиболее полное впечатление о программе: он будет посвящен как принципам и основам работы с Maxima, так и описанию более широких ее возможностей и практическим примерам.
Пару слов о программе
На данный момент Maxima выпускается под две платформы: Unix-совместимые системы, т.е. Linux и *BSD, и MS Windows. Я, конечно же, буду вести речь о Linux-версии.
Сама по себе Maxima – консольная программа, и все математические формулы отрисовывает обычными текстовыми символами. В этом есть как минимум два плюса. С одной стороны, саму Maxima можно использовать как ядро, надстраивая поверх нее графические интерфейсы на любой вкус. Их на сегодняшний день существует немало; в этот раз я остановлюсь на двух самых популярных (см. врезку) – и наиболее наглядных и удобных в работе, а об остальных поговорим в следующих выпусках; они тоже по-своему интересны, хотя более специфичны.
С точки зрения ознакомления с самой Maxima наибольший интерес представляют два интерфейса.
Первый – это отдельная самостоятельная графическая программа по имени wxMaxima (рис. 1). Она, как и сама Maxima, помимо Linux/*BSD существует еще и в версии для MS Windows. В wxMaxima вы вводите формулы в текстовом виде, а вывод Максимы отображается графически, привычными математическими символами. Кроме того, большой упор здесь сделан на удобство ввода: командная строка отделена от окна ввода-вывода, а дополнительные кнопки и система меню позволяют вводить команды не только в текстовом, но и в диалоговом режиме. Так называемое «автодополнение» в командной строке на самом деле с таковым имеет лишь то сходство, что вызывается клавишей «Tab». Ведет же оно себя, к сожалению, всего лишь как умная история команд, т.е. вызывает ту команду из уже введенных в этой сессии, которая начинается с заданных в командной строке символов, но не дополняет до имен команд и их параметров. Таким образом, этот интерфейс наиболее удобен в том случае, когда вам нужно много вычислять и видеть результаты на экране; и еще, возможно, в том случае, если вы не очень любите вводить все команды с клавиатуры. Кроме того, wxMaxima предоставляет удобный интерфейс к документации по системе; хотя, так как документация поставляется в формате html, вместо этого можно использовать обычный браузер.
Второй достаточно интересный интерфейс к Maxima – это дополнительный режим в редакторе TeXmacs. Хотя этот редактор имеет общее историческое прошлое с широко известным Emacs, что явствует из названия, но практического сходства между ними мало. TeXmacs разрабатывается для визуального редактирования текстов научной тематики, при котором вы видите на экране редактируемый текст практически в том же виде, в котором он будет распечатан. В частности, он имеет так называемый математический режим ввода, очень удобный для работы с самыми разнообразными формулами, и умеет импортировать/экспортировать текст в LaTeX и XML/HTML. Именно возможностями по работе с формулами пользуется Maxima, вызванная из TeXmacs’а. Фактически, формулы отображаются в привычной математической нотации, но при этом их можно редактировать и копировать в другие документы наподобие обыкновенного текста. Maxima-сессия вызывается из меню: «Вставить–>Сессия–>Maxima», при этом появляется дополнительное меню с командами Максимы. После запуска сессии можно уже внутри нее перейти в математический режим ввода (меню режимов ввода вызывается первой кнопкой на панели ввода) и при вводе также использовать элементы математической нотации (рис. 2). Этот интерфейс будет наиболее удобен тем, кто хочет использовать результаты вычислений в своих текстах и любит редактировать их в визуальном режиме.
С другой стороны, сама по себе, без каких-либо интерфейсных надстроек, Maxima нетребовательна к железу и может работать на таких компьютерах, которые сейчас и за компьютеры уже никто не считает (это может оказаться актуальным, к примеру, для вуза или научной лаборатории, у которых денег на обновление парка машин скорее всего нет, а потребность в ПО для символьных вычислений возникнуть может).
Имена функций и переменных в Максиме чувствительны к регистру, то есть прописные и строчные буквы в них различаются. Это не будет в новинку любому, кто уже имел дело с POSIX-совместимыми системами или с такими языками программирования, как, скажем, C или Perl. Удобно это и с точки зрения математика, для которого тоже привычно, что заглавными и строчными буквами могут обозначаться разные объекты (например, множества и их элементы, соответственно).
Для того, чтобы начать работать с программой, вам понадобится пакет Maxima; если в стандартных репозитариях вашего дистрибутива его не окажется, то взять его можно на сайте проекта, адрес которого приведен во врезке.
Принципы работы с программой не зависят от того, какой интерфейс к ней вы выберете, поэтому я постараюсь максимально абстрагироваться от конкретного интерфейса, ограничиваясь лишь небольшими комментариями в тех случаях, когда они ведут себя по-разному.
На данный момент последняя версия программы – 5.9.3, именно о ней я и буду говорить; если в вашем дистрибутиве пока присутствует более старая версия, вы в принципе можете использовать ее: и актуальная еще несколько месяцев назад 5.9.2, и вышедшая в конце прошлого года 5.9.1 не имеют с нынешней принципиальных различий.
Приступаем к работе
После запуска Maxima-сессии мы видим перед собой такие строки:
Maxima restarted. (%i1)
Первая – это сообщение о том, что ядро Максимы только что запустилось (вместо нее, в зависимости от версии и конкретной сборки, может выводиться краткая информация о программе); вторая – приглашение к вводу первой команды. Команда в Максиме – это любая комбинация математических выражений и встроенных функций, завершенная, в простейшем случае, точкой с запятой. После ввода команды и нажатия «Enter» Maxima выведет результат и будет ожидать следующей команды:
Для арифметических действий используются традиционные обозначения: –, +, *, /; ** или ^ для возведения в степень, sqrt() для квадратного корня.
Далее я часто буду пользоваться для наглядности упомянутым во врезке математическим режимом ввода редактора TeXmacs. К примеру, приведенный выше код выглядел бы так:
Если для каких-то обозначений будет неочевидно, как записать их в строку, я буду пояснять это по ходу изложения. Как видите, каждая ячейка имеет свою метку; эта метка – заключенное в скобки имя ячейки. Ячейки ввода именуются как %i с номером (i от input – ввод), ячейки вывода – как %o с соответствующим номером (o от output – вывод). Со знака % начинаются все встроенные служебные имена: чтобы, с одной стороны сделать их достаточно короткими и удобными в использовании, а с другой – избежать возможных накладок с пользовательскими именами, которые тоже часто удобно делать короткими. Благодаря такому единообразию вам не придется запоминать, как часто бывает в других системах, какие из таких коротких и удобных имен зарезервированы программой, а какие вы можете использовать для своих нужд. К примеру, внутренними именами %e и %pi обозначены общеизвестные математические постоянные; а через %c с номером обозначаются константы, используемые при интегрировании, для которых использование буквы «c» традиционно в математике.
При вводе мы можем обращаться к любой из предыдущих ячеек по ее имени, подставляя его в любые выражения. Кроме того последняя ячейка вывода обозначается через %, а последняя ячейка ввода – через _. Это позволяет обращаться к последнему результату, не отвлекаясь на то, каков его номер.
Здесь %+47/59 – то же самое, что %o1+47/59.
Вывод результата вычисления не всегда нужен на экране; его можно заглушить, завершив команду символом $ вместо ;. Заглушенный результат при этом все равно вычисляется; как видите, в этом примере ячейки %o1 и %o2 доступны, хотя и не показаны (к ячейке %o2 обращение идет через символ %, смысл которого расшифрован выше):
Каждую следующую команду не обязательно писать с новой строки; если ввести несколько команд в одну строчку, каждой из них все равно будет соответствовать свое имя ячейки. К примеру, здесь в строке после метки %i1 введены ячейки от %i1 до %i4; в ячейке %i3 используются %i1 и %i2 (обозначенная как _ – предыдущий ввод):
В wxMaxima и TeXmacs последнюю или единственную команду в строке можно не снабжать завершающим символом – это сработает так же, как если бы она была завершена ; , т.е. вывод заглушен не будет. В дальнейших примерах я часто буду опускать ; . Если вы выберете другой интерфейс, не забывайте ее добавлять.
Помимо использования имен ячеек, мы, естественно, можем и сами давать имена любым выражениям. По-другому можно сказать, что мы присваиваем значения переменным, с той разницей, что в виде значения такой переменной может выступать любое математическое выражение. Делается это с помощью двоеточия – знак равенства оставлен уравнениям, которые, учитывая общий математический контекст записи, проще и привычнее так читаются. И к тому же, так как основной конек Максимы – символьная запись и аналитические вычисления, уравнения достаточно часто используются. Например:
В каком-то смысле двоеточие даже нагляднее в таком контексте, чем знак равенства: это можно понимать так, что мы задаем некое обозначение, а затем через двоеточие расшифровываем, что именно оно обозначает. После того, как выражение поименовано, мы в любой момент можем вызвать его по имени:
Любое имя можно очистить от присвоенного ему выражения функцией kill(), и освободить занимаемую этим выражением память. Для этого нужно просто набрать kill(name), где name – имя уничтожаемого выражения; причем это может быть как имя, назначенное вами, так и любая ячейка ввода или вывода. Точно так же можно очистить разом всю память и освободить все имена, введя kill(all). В этом случае очистятся в том числе и все ячейки ввода-вывода, и их нумерация опять начнется с единицы. В дальнейшем, если по контексту будет иметься в виду логическое продолжение предыдущих строк ввода-вывода, я буду продолжать нумерацию (этим приемом я уже воспользовался выше). Когда же новый «сеанс» будет никак не связан с предыдущим, буду начинать нумерацию заново; это будет косвенным указанием сделать «kill(all)», если вы будете набирать примеры в Maxima, так как имена переменных и ячеек в таких «сеансах» могут повторяться.
Доступ к документации Максимы
В примерах выше мы воспользовались двумя встроенными функциями. Как нетрудно догадаться из контекста, solve – это функция решения уравнения, а diff – функция дифференцирования. Практически весь функционал Maxima реализован через такие встроенные функции. Функция в Maxima может иметь переменное число аргументов. Например, функция solve, которую мы использовали с одним аргументом, чаще вызывается с двумя аргументами. Первый задает уравнение или функцию, чьи корни надо найти; второй – переменную, относительно которой нужно решать уравнение:
Если формула, задающая решаемое уравнение, содержит только один символ, как в предыдущем примере, то второй аргумент можно опустить, так как выбор, относительно чего нужно решать уравнение, все равно однозначен.
Вторая функция из наших новых знакомых – diff – также может принимать один аргумент; в этом случае она находит дифференциал заданного выражения:
Через del(x) и del(y) здесь обозначены дифференциалы соответствующих символов.
Для каждой встроенной функции есть описание в документации по Maxima. Оно содержит сведения о том, какие аргументы и в каких вариантах принимает функция, а также описание ее действия в разных случаях и конкретные примеры применения. Но, конечно, искать описание каждой нужной функции в html-документации или info-страницах не всегда удобно, тем более, что нужна эта информация, как правило, прямо в процессе работы. Поэтому в Maxima есть специальная функция – describe(), – которая выдает информацию из документации по конкретным словам. Более того, специально для удобства получения справочной информации существует сокращенная версия вызова этой функции: ? name вместо describe(name). Здесь ? – это имя оператора, и аргумент нужно отделять от него пробелом (выражение ?name используется для вызова функции Lisp с именем name). Функция describe и оператор ? выдают список тех разделов помощи и имен функций, которые содержат заданный текст, после чего предлагают ввести номер того раздела или описания той функции, которые вы хотите посмотреть:
Когда вы выберете раздел, будет выдано его содержимое:
Если для слова, которое вы ввели после ? или describe, найдено единственное совпадение, его описание будет показано сразу.
Кроме справки, по многим функциям Maxima есть примеры их использования. Пример можно загрузить функцией example(). Вызов этой функции без аргумента отобразит список всех имен доступных примеров; вызов вида example(name) загрузит в текущую сессию и выполнит указанный файл примера:
Основные принципы
- Сайт проекта Maxima: http://maxima.sourceforge.net/
- Сайт wxMaxima: http://wxmaxima.sourceforge.net/
- Сайт редактора TeXmacs: http://www.texmacs.org/
- Web-интерфейс к Максиме: http://www.et.byu.edu/~koj/maxima.html
То, что Максима написана на Lisp, человеку, знакомому с этим языком, становится понятно уже в начале работы с программой. Действительно, в Максиме четко прослеживается «лисповский» принцип работы с данными, который оказывается очень кстати в контексте символьной математики и аналитических вычислений. Дело в том, что в Lisp, по большому счету, нет разделения на объекты и данные: имена переменных и выражения могут использоваться практически в одном и том же контексте. В Maxima же это свойство развито еще сильнее: фактически, мы можем использовать любой символ вне зависимости от того, присвоено ли ему какое-то выражение. По умолчанию символ, связанный с любым выражением, будет представлять это выражение; символ, не связанный ни с чем, будет представлять самого себя, трактуемого опять-таки как выражение. Поясним на примере:
Из этого следует, в частности, что в выражение автоматически подставляется значение входящего в него символа только в том случае, если это значение было приписано символу до определения выражения:
Если некоторый символ уже имеет какое-то значение, можем ли мы использовать в выражении сам этот символ, а не его значение? Конечно. Сделать это можно с помощью знака апострофа – введенный перед любым символом или выражением, он предотвращает его вычисление:
Результат выражения %i12 был бы аналогичен и в том случае, если бы b и y не имели на тот момент никаких значений; таким образом, мы можем смело блокировать вычисление символа, даже не запоминая (или не зная), присвоены ли им вообще какие-то выражения.
Точно так же можно поступить с любой встроенной функцией, если мы хотим не выполнить ее, а использовать в своем математическом контексте. Например, уже упомянутая функция дифференцирования может пригодиться нам для обозначения производной в дифференциальном уравнении; в этом случае, конечно, вычислять ее не надо:
Благодаря описанным особенностям работа в Максиме, с одной стороны, становится во многом похожей на традиционную «ручную» работу с математическими формулами, что практически сводит на нет психологический барьер в начале работы с программой. С другой стороны, даже на этом начальном этапе вы фактически избавлены от наиболее рутинной ручной работы, вроде отслеживания текущих значений символов, и можете полностью сосредоточиться на самой задаче.
Конечно, блокировка вычислений – это не единственный способ влиять на то, как Максима будет вычислять то или иное выражение; этим процессом можно управлять довольно гибко.
О существовании так называемых «живых CD-дистрибутивов» (LiveCD) Linux, способных загружаться и работать прямо с компакт-диска, слышали в наше время почти все. Один из самых популярных среди этой братии – дистрибутив Knoppix, основанный на Debian, – в особом представлении тоже, я думаю, не нуждается. А вот среди специализированных LiveCD-дистрибутивов, основанных уже на Knoppix’е (которых последнее время тоже, признаться, развелось немало) мне попался один очень интересный экземпляр, узнать о котором можно разве что случайно. А дистрибутив этот действительно интересен, потому как предоставляет возможность познакомиться «живьем», без установки, с многочисленными и разнообразными программами весьма полезного и в то же время не слишком широко известного профиля – компьютерной математикой. Называется он – соответственно своей профессии – Knoppix-math.
Основан этот дистрибутив, если говорить точно, не на самом Knoppix’е, а на Knoppix-ja, т.е. его японском варианте. Не бойтесь, японский язык учить не придется – английский вариант интерфейса также присутствует (хотя не исключено, что именно происхождение виной малой популярности дистрибутива в Европе).
Самую свежую на данный момент англоязычную информацию о дистрибутиве можно найти по этому адресу: http://geom.math.metro-u.ac.jp/wiki/index.php?KNOPPIX/Math/English
В частности, в разделе Download есть ссылки на пять зеркал, содержащих образы компакт-дисков. Качать советую последнюю японскую версию – английская уже порядком устарела, а англоязычный интерфейс, как я уже говорил, и в японской присутствует. Для того, чтобы его выбрать, всего лишь надо ввести при загрузке knoppix lang=en или, чтобы получить в списке доступных раскладок клавиатуры русскую, knoppix lang=ru (интерфейс при этом также будет английский). Последняя версия выпущена в феврале этого года и основана на Knoppix 4.0.2. Прямые ссылки на образ диска и его контрольную сумму на одном из зеркал:
- ftp://fun.sci.fukuoka-u.ac.jp/pub/knoppix/knoppix_v4.0.2-math-20060217-ja.iso
- ftp://fun.sci.fukuoka-u.ac.jp/pub/knoppix/knoppix_v4.0.2-math-20060217-ja.iso.md5
Диск содержит более тридцати математических программ, среди которых такие известные, как Maxima, GNUplot, Octave, Yorick, GNU R, TeXmacs. Кроме того, присутствуют и языки программирования Python, Ruby и Tcl/tk; и, конечно же, TeX.
Помимо ПО математического профиля, есть на диске и программы общего назначения: OpenOffice.org, Kate и KWrite; xpdf, Kuickshow и ImageMagic; Mozilla Firefox и Konqueror. Т.е. все для полноценного рабочего места. И все это может работать в обрамлении любого из традиционной уже для Knoppix’а тройки: KDE, IceWM и Fluxbox.
Возможно, вы захотите воспользоваться этим LiveCD, чтобы познакомиться с программой символьных вычислений Maxima, цикл статей о которой начинается в этом номере, и каким-либо графическим интерфейсом к ней – многие из них тоже доступны на диске.
Так как в этом цикле статей речь пойдет о математической программе для символьных вычислений, для начала пару слов о том, что из себя представляют эти самые символьные или, как их еще называют, аналитические вычисления, в отличие от численных расчетов. Компьютеры, как известно, оперируют с числами (целыми и с плавающей запятой). К примеру, решения уравнения можно получить как -0.41421356 и 2.41421356, а 3x=1 – как 0.33333333. А ведь хотелось бы увидеть не приближенную цифровую запись, а точную величину, т.е. в первом случае и во втором. С этого простейшего примера и начинается разница между численными и символьными вычислениями. Но кроме этого, есть еще задачи, которые вообще невозможно решить численно. Например, параметрические уравнения, где в виде решения нужно выразить неизвестное через параметр; или нахождение производной от функции; да практически любую достаточно общую задачу можно решить только в символьном виде. Поэтому неудивительно, что и для такого класса задач появились компьютерные программы, оперирующие уже не только числами, а почти любыми математическими объектами, от векторов до тензоров, от функций до интегро-дифференциальных уравнений и т.д.
История проекта, известного ныне под именем Maxima, началась еще в конце 60-х годов в легендарном MIT (Massachusetts Institute of Technology – Массачусетский Технологический Институт), когда в рамках существовавшего в те годы большого проекта MAC началась работа над программой символьных вычислений, которая получила имя Macsyma (от MAC SYmbolic MAnipulation). Архитектура системы была разработана к июлю 1968 г., непосредственно программирование началось в июле 1969. В качестве языка для разработки системы был выбран Lisp, и история показала, насколько это был правильный выбор: из существующих в то время языков программирования он единственный продолжает развиваться и сейчас – спустя почти полвека после старта проекта. Принципы, положенные в основу проекта, позднее были заимствованы наиболее активно развивающимися ныне коммерческими программами – Mathematica и Maple; таким образом, Macsyma фактически стала родоначальником всего направления программ символьной математики. Естественно, Macsyma была закрытым коммерческим проектом; его финансировали государственные и частные организации, среди которых были вошедшее в историю ARPA (Advanced Research Projects Agency; помните ARPAnet – предок интернета?), Энергетический и Оборонный Департаменты США (Departments of Energy & Defence, DOE and DOD). Проект активно развивался, а организации, контролирующие его, менялись не раз, как это всегда бывает с долгоживущими закрытыми проектами. В 1982 году профессор Уильям Шелтер (William Schelter) начал разрабатывать свою версию на основе этого же кода, под названием Maxima. В 1998 году Шелтеру удалось получить от DOE права на публикацию кода по лицензии GPL. Первоначальный проект Macsyma прекратил свое существование в 1999 году. Уильям Шелтер продолжал заниматься разработкой Maxima вплоть до своей смерти в 2001 году. Но, что характерно для открытого ПО, проект не умер вместе со своим автором и куратором. Сейчас проект продолжает активно развиваться, и участие в нем является лучшей визитной карточкой для математиков и программистов всего мира.
Если у вас возникли проблемы с запуском Maxima- сессии из TeXmacs, обратите внимание на то, кто у вас в системе выступает под именем /bin/sh. Дело в том, что инициализация всех разнообразных сессий реализована в TeXmacs’е через shell-скрипты, вызываемые именно с помощью /bin/sh. И в скрипте, отвечающем за сессию Maxima, используется возможность, которая не стандартизирована как обязательная для /bin/sh, но присутствует в его эмуляции bash. Другими словами, если у вас /bin/sh является не ссылкой на /bin/bash, а чем-то другим, то именно это может послужить причиной невозможности открыть Maxima-сессию (к примеру, в Debian и основанных на нем дистрибутивах кроме bash ссылку /bin/sh на себя может захотеть поставить еще и более легкий dash; в этом случае восстановить статус-кво можно с помощью dpkg-reconfigure dash). Если сделать /bin/sh ссылкой на /bin/bash не представляется возможным, можете попробовать поменять #!/bin/sh на #!/bin/bash в файле /usr/lib/texmacs/TeXmacs/bin/maxima_detect. Я написал об этой проблеме разработчикам TeXmacs, но еще не получил никакой их реакции, так что не могу пока сказать, будет ли исправлена эта недоработка в ближайших версиях.